Published online by Cambridge University Press: 12 March 2014
The principal aim of this paper is to establish a theorem stating, roughly, that the addition of the fan theorem and the. continuity schema to an intuitionistic system of elementary analysis results in a conservative extension with respect to arithmetical statements.
The result implies that the consistency of first order arithmetic cannot be proved by use of the fan theorem, in addition to standard elementary methods—although it was the opposite assumption which led Gentzen to withdraw the first version of his consistency proof for arithmetic (see [B]).
We must presuppose acquaintance with notation and principal results of [K, T], and with §1.6, Chapter II, and Chapter III, §4-6 of [T1]. In one respect we shall deviate from the notation in [K, T]: We shall use (n)x (instead of g(n, x)) to indicate the xth component of the sequence coded by n, if x < lth(n), 0 otherwise.
We also introduce abbreviations n ≤* m, a ≤ b which will be used frequently below:
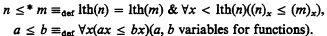
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.