No CrossRef data available.
Article contents
Complete types and the natural numbers
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper it is shown that, for any complete type Σ omitted in the structure 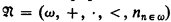 , or in any expansion
, or in any expansion 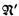 of
of 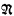 having only countably many relations and operations, there is a proper elementary extension
having only countably many relations and operations, there is a proper elementary extension 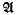 of
of 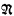 (or of
(or of 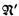 ) which omits Σ. This result (which was announced in [2]) is used to answer a question of Malitz on complete
) which omits Σ. This result (which was announced in [2]) is used to answer a question of Malitz on complete 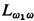 -sentences. The result holds also for countable families of types.
-sentences. The result holds also for countable families of types.
A type is a countable set of formulas with just the variable υ free. A structure 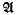 is said to omit a type Σ if no element of
is said to omit a type Σ if no element of 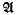 satisfies all of the formulas of Σ. For example,
satisfies all of the formulas of Σ. For example, 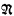 omits the type Σω = {υ ≠ n: n ∈ ω}, since n fails to satisfy υ ≠ n. (Here n is the constant symbol standing for n.)
omits the type Σω = {υ ≠ n: n ∈ ω}, since n fails to satisfy υ ≠ n. (Here n is the constant symbol standing for n.)
A type Σ is said to be complete with respect to a theory T if the set of sentences T ∪ Σ(e) generates a complete theory, where Σ(e) is the result of replacing υ by the new constant e in all of the formulas of Σ. The type Σω is clearly not complete with respect to Th(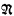 ). (For any structure Th(
). (For any structure Th(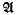 ), Th(
), Th(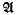 ) is the set of all sentences true in
) is the set of all sentences true in 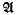 .)
.)
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1973


