Published online by Cambridge University Press: 12 March 2014
Notations, conventions, and definitions. {μi∣i < ω} will be an effective enumeration of all partial recursive μi{ω → 2. A type of a theory T will be a set of formulas in the language of T, in finitely many free variables, which is consistent with T. A complete type is a maximal type in some fixed number of free variables. A type is recursive if, relative to some effective enumeration of the formulas of the language, the characteristic function for the type is recursive. A set ψ of recursive types has property P if some set of indices of characteristic functions for all the types in ψ has property P. So, for example, we might say that a set of recursive types is 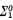 . If
. If 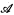 is an L-structure, then the type spectrum of
is an L-structure, then the type spectrum of 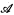 , denoted ‘TySp(
, denoted ‘TySp(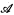 )’, is the set of complete types realized in
)’, is the set of complete types realized in 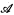 (we will assume that an n-type has formulas with free variables among {x1, …, xn}). A type spectrum for a theory T is a type spectrum of some model of T. ‘TySp0(T)’ will denote the set of principal types of T.
(we will assume that an n-type has formulas with free variables among {x1, …, xn}). A type spectrum for a theory T is a type spectrum of some model of T. ‘TySp0(T)’ will denote the set of principal types of T.
We will assume that the reader is familiar with Henkin constructions of models, and of passing from a maximal consistent set of sentences, with “Henkin constants”, to a model. In particular, for a theory T in L we will let {ai∣i < ω} be new distinct constant symbols, and {φi < ω} a list of all sentences in the expanded language. ‘ΔN’ will denote the elementary diagram constructed at stage N, and 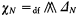 .
.
The preparation of this paper was partially supported by Grant NSF-MCS77-0O802.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.