L denotes a fixed finitary similarity type, B, respectively P a new relation symbol, 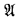an L-structure in the usual sense, and (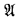, σ) a topological L-structure, where σ is a topology on A. (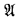, σ) is countable if 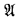is countable and σ has a countable base. The formal language for our study of topological structures is 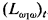. 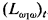is the least fragment of the (monadic) second-order, infinitary language 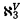closed under negation (⇁), countable disjunction (∨), countable conjunction (∧), quantification over individual variables (∃ν, ∀ν), and quantification over set variables in the form ∃V(t ∈ V → φ) [respectively ∃V(t ∈ V → φ] where t is an L-term and each free occurrence of V in φ is negative [respectively positive]. We abbreviate ∃V(t ∈ V ∧ φ) and ∀V(t ∈ V → φ) by ∃V ∈ ν φ respectively ∀V ∈ ν φ. (For detailed information on 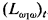we reIer to [1].)

i, j, … m, n range over ω. a, x, etc. denote finite tuples; a ∈ A means that all members of a are in A. IdA denotes the identity on A, Perm(A) the set of all permutations of A, and Aut(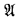) (respectively Aut(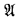, σ)) the set of all automorphisms of 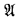(respectively (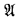σ)). Let F ⊆ Perm(A), B ⊆ Am(m ≥ 1), and μ be a system of subsets of A. B (respectively μ) is called invariant under F if for all ƒ ∈ F, ƒ(B) = B (respectively ƒ(μ) = μ). 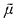denotes the least system of subsets of A which contains μ and which is closed under arbitrary union, .

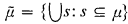For the rest of this paragraph let A be a countable nonempty set.