Article contents
Sentences implying their own provability
Published online by Cambridge University Press: 12 March 2014
Extract
We begin with a simple observation and a simple question. If we fix Th(x), some reasonable formulation of “x is the Gödel number of a theorem of Peano Arithmetic”, then for any 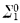 sentence σ, Peano Arithmetic proves σ → Th(⌈σ⌉). (Here ⌈σ⌉ is the canonical term denoting the Gödel number of σ.) This observation is crucial to the proof of the Second Incompleteness Theorem. Call ψ a self-prover (with respect to Th(x)) if ψ → Th(⌈ψ⌉) is a theorem of Peano Arithmetic (from now on, PA). Our simple question is this: Does the observation have a converse—must every self-prover be provably equivalent to a
sentence σ, Peano Arithmetic proves σ → Th(⌈σ⌉). (Here ⌈σ⌉ is the canonical term denoting the Gödel number of σ.) This observation is crucial to the proof of the Second Incompleteness Theorem. Call ψ a self-prover (with respect to Th(x)) if ψ → Th(⌈ψ⌉) is a theorem of Peano Arithmetic (from now on, PA). Our simple question is this: Does the observation have a converse—must every self-prover be provably equivalent to a 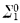 sentence? Whatever φ happens to be, the formula φ ∧ Th(⌈φ⌉) is a self-prover. This makes it seem clear that there must exist self-provers which are not provably
sentence? Whatever φ happens to be, the formula φ ∧ Th(⌈φ⌉) is a self-prover. This makes it seem clear that there must exist self-provers which are not provably 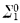 : We need only use a suitably complicated φ.
: We need only use a suitably complicated φ.
Deciding what sort of complication is “suitable” and finding such a φ is surprisingly annoying. Here is a quick example: One might guess that any φ which is unprovable and 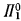 would work. In that case we could take φ to be CON—that is, ¬Th(⌈0 = 1⌉); but CON ∧ Th(⌈CON⌉) is refutable in PA, so is provably equivalent to the quantifier-free formula 0 = 1.
would work. In that case we could take φ to be CON—that is, ¬Th(⌈0 = 1⌉); but CON ∧ Th(⌈CON⌉) is refutable in PA, so is provably equivalent to the quantifier-free formula 0 = 1.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
References
BIBLIOGRAPHY
- 9
- Cited by


