Published online by Cambridge University Press: 12 March 2014
Throughout, M will denote a transitive model of ZFC. Using the terms “random” and “generic” in the sense of [1], one may ask whether there can exist real numbers x and y such that x is generic over M[y] and y is random over M[x]. We shall see below by an elementary argument that this is not possible, and so, in a crude sense at least, random and generic extensions do not commute. This does not however rule out the possibility of a weaker commutativity. Let B be the complete Boolean algebra (in M) for adjoining a random real followed by a generic real and C be the complete Boolean algebra for adjoining a generic real followed by a random real. Then it still might be the case that B and C are isomorphic. This also fails, though, and we shall prove this by establishing the following combinatorial properties of MB and MC:

but
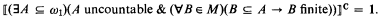
In addition this will show that C cannot be embedded as a complete subalgebra of B.
The property satisfied by B is reminiscent of calibre ℵ1 [2]. B would have calibre if we could replace “infinite” by “uncountable”, and this occurs if Martin's Axiom 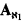 holds in M. To obtain the nonisomorphism of B and C in general necessitated looking at the weaker property.
holds in M. To obtain the nonisomorphism of B and C in general necessitated looking at the weaker property.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.