Published online by Cambridge University Press: 12 March 2014
We conclude here the treatment of forcing in recursion theory begun in Part I and continued in Part II of [31]. The numbering of sections is the continuation of the numbering of the first two parts. The bibliography is independent.
In Part I our language was a first-order language: the only set we considered was the (set constant for the) generic set. In Part II a second-order language was introduced, and we had to interpret the second-order variables in some way. What we did was to consider the ramified analytic hierarchy, defined by induction as:
A0 = {X ⊆ ω: X is arithmetic},
Aα+1 = {X ⊆ ω: X is definable (in 2nd order arithmetic) over Aα},
Aλ = ⋃α<λAα (λ limit),
RA = ⋃αAα.
We then used (a relativized version of) the fact that 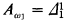 (Kleene [27]). The definition of RA is obviously modeled on the definition of the constructible hierarchy introduced by Gödel [14]. For this we no longer work in a language for second-order arithmetic, but in a language for (first-order) set theory with membership as the only nonlogical relation:
(Kleene [27]). The definition of RA is obviously modeled on the definition of the constructible hierarchy introduced by Gödel [14]. For this we no longer work in a language for second-order arithmetic, but in a language for (first-order) set theory with membership as the only nonlogical relation:
L0 = ⊘,
Lα+1 = {X: X is (first-order) definable over Lα},
Lλ = ⋃α<λLα (λ limit),
L = ⋃αLα.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.