Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-19T03:42:14.488Z Has data issue: false hasContentIssue false
  • English
  • Français

State-strategies for games in Fσδ ∩ Gδσ

Published online by Cambridge University Press:  12 March 2014

J. Richard Büchi
J. Richard Büchi*
Affiliation:
Purdue University, West Lafayette, Indiana 47907
Get access Rights & Permissions [Opens in a new window]

Extract

The Cantor-Bendixson theorem says: For every closed set 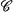, ∣∣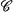 ≤ ω0 ∨ 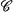⊇ perfect (and therefore 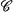is countable or has the power of the continuum). W. H. Young proved the alternative for Gδ-sets, and Hausdorff extended it to Souslin-sets. Cantor used his ordinals to prove the theorem (I like to think he invented them for this purpose). In Hausdorff's Mengenlehre ordinals do not officially enter in either of the three proofs. You should try to put them back. It is very important never to hide away ω1 when it actually is there, and it is there when the continuum problem is the subject.

In Davis [6] you find that Cantor's alternative is equivalent to another alternative: (I wins 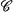) ∨ (J wins 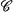). Here 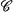means a lopsided game in which one of the players makes long moves on the game tree. So, the classical theorems can be restated as determinacy results for lopsided games, and now I make this observation: The original CB-proof “actually presents” a winning strategy. The HD-proofs do no such thing; all you know at the end is existence of a winning strategy (and Davis' remark is needed to gain this knowledge).

You understand now why I like CB-proofs, particularly for determinacy of games. They do exist also for games in which both players make short moves. Many years ago I tried to publish such a proof for determinacy of Fσ-games. The referee said it was not worth the trouble. I say you should remake this proof (it is a special case of the one presented in this paper), because it is the ideal of a determinacy proof.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 4 , December 1983 , pp. 1171 - 1198
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Büchi, J.R., Weak second order arithmetic andfinite automata, Zeitschrift fur Mathematische Logik und Grundlagen der Mathematik, vol. 6 (1960), pp. 66–92.CrossRefGoogle Scholar
[2]Büchi, J.R., On a decision method in restricted second order arithmetic, Proceedings of 1960 International Congress for Logic, Methodology and the Philosophy of Science, Stanford University Press, Stanford, Calif., 1962, pp. 1–11.Google Scholar
[3]Büchi, J.R., The monadic second order theory of ω1, Lecture Notes in Mathematics, vol. 328, Springer-Verlag, Berlin and New York, 1973, pp. 1–127.Google Scholar
[4]Büchi, J.R., Using determinancy of games to eliminate quantifiers, Fundamentals of Computation Theory, Lecture Notes in Mathematics, vol. 56, Springer-Verlag, Berlin and New York, 1977, pp. 367–378.CrossRefGoogle Scholar
[5]Büchi, J.R. and Landweber, L.H., Solving sequential conditions by finite state operators, Transactions of the American Mathematical Society, vol. 138 (1969), pp. 295–311.CrossRefGoogle Scholar
[6]Davis, M., Infinite games of perfect information, Advances in Game Theory, Annals of Mathematical Studies, no. 52 (1964), pp. 85–101.Google Scholar
[7]Elgot, C.C., Decision problems of finite automata design and related arithmetics, Transactions of the American Mathematical Society, vol. 98 (1961), pp. 21–51.CrossRefGoogle Scholar
[8]Feferman, S. and Vaught, R.L., The first order properties of products of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[9]Löwenheim, L., Über Möglichkeiten im Relativkalkul, Mathematische Annalen, Band 76 (1915), pp. 447–470.CrossRefGoogle Scholar
[10]McNaughton, R., Testing and generating infinite sequences by finite automata, Information and Control, vol. 9 (1966), pp. 521–530.CrossRefGoogle Scholar
[11]Martin, D. A., Borel determinacy, Annals of Mathematics (2), vol. 102 (1975), pp. 363–371.CrossRefGoogle Scholar
[12]Rabin, M.O., Decidability of second-order theories and automata on infinite trees, Transactions of the American Mathematical Society, vol. 141 (1969), pp. 1–35.Google Scholar
[13]Robinson, R.M., Restricted set theoretical definitions in arithmetic, Proceedings of the American Mathematical Society, vol. 9 (1958), pp. 238–242.CrossRefGoogle Scholar
[14]Shelah, S., The monadic theory of order, Annals of Mathematics (2), vol. 102 (1975), pp. 379–419.CrossRefGoogle Scholar
[15]Skolem, Th., Untersuchungen über die Axiome des Klassenkalkuls ünd Uber Produktations-undSummationsprobleme welche gewisse Klassen von Aussagen betreffen, Skrifter utgit av Viden-skapsselskapet i Kristiana. I: Matematisk-naturvidenskalbelig Klasse 1919, no. 3.Google Scholar