Published online by Cambridge University Press: 12 March 2014
If κ is a measurable cardinal, then it is a well-known fact that there is at least one normal ultrafilter over κ. In [K-1], Kunen showed that one cannot say more without further assumptions, for if U is a normal ultrafilter over κ, then L[U] is an inner model of ZFC in which κ has exactly one normal measure. On the other hand, Kunen and Paris showed [K-P] that if κ is measurable in the ground model, then there is a forcing extension in which κ has 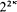 normal ultrafilters, so it is consistent that κ has the maximum possible number of normal ultrafilters. Starting with assumptions stronger than measurability, Mitchell [Mi-1] filled in the gap by constructing models of ZFC + GCH satisfying “there are exactly λ normal ultrafilters over κ”, where λ could be κ+ or κ++ (measured in the model), or anything ≤ κ. Whether or not Mitchell's results can be obtained by starting only with a measurable cardinal in the ground model and defining a forcing extension is unknown.
normal ultrafilters, so it is consistent that κ has the maximum possible number of normal ultrafilters. Starting with assumptions stronger than measurability, Mitchell [Mi-1] filled in the gap by constructing models of ZFC + GCH satisfying “there are exactly λ normal ultrafilters over κ”, where λ could be κ+ or κ++ (measured in the model), or anything ≤ κ. Whether or not Mitchell's results can be obtained by starting only with a measurable cardinal in the ground model and defining a forcing extension is unknown.
There are substantial differences between the Mitchell models and the Kunen-Paris models. In the Kunen-Paris models κ can be the only measurable cardinal. However, in the Mitchell model in which κ has exactly 2 normal ultrafilters, one of them contains the set {α < κ: α is measurable} while the other does not. Thus it is natural to ask if it is possible to get a model M of ZFC in which κ is the only measurable cardinal and κ has exactly 2 normal ultrafilters. In this paper we will show that, using appropriate large cardinal assumptions, the answer is yes.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.