Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-19T01:18:51.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Why some people are excited by Vaught's conjecture

Published online by Cambridge University Press:  12 March 2014

Daniel Lascar
Daniel Lascar*
Affiliation:
UER de Mathématique et Informatique, Université Paris VII, Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

§I. In 1961, R. L. Vaught ([V]) asked if one could prove, without the continuum hypothesis, that there exists a countable complete theory with exactly ℵ1 isomorphism types of countable models. The following statement is known as Vaught conjecture:

Let T be a countable theory. If T has uncountably many countable models, then T has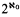countable models.

More than twenty years later, this question is still open. Many papers have been written on the question: see for example [HM], [M1], [M2] and [St]. In the opinion of many people, it is a major problem in model theory.

Of course, I cannot say what Vaught had in mind when he asked the question. I just want to explain here what meaning I personally see to this problem. In particular, I will not speak about the topological Vaught conjecture, which is quite another issue.

I suppose that the first question I shall have to face is the following: “Why on earth are you interested in the number of countable models—particularly since the whole question disappears if we assume the continuum hypothesis?” The answer is simply that I am not interested in the number of countable models, nor in the number of models in any cardinality, as a matter of fact. An explanation is due here; it will be a little technical and it will rest upon two names: Scott (sentences) and Morley (theorem).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 4 , December 1985 , pp. 973 - 982
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Barwise, J., Back and forth through infinitary logic, Studies in model theory (Morley, M., editor), Mathematical Association of America, Buffalo, New York, 1973, pp. 5–34.Google Scholar
[Bo]Bouscaren, E., Martin's conjecture for ω-stable theories, Israel Journal of Mathematics, vol. 49 (1984), pp. 15–25.CrossRefGoogle Scholar
[HM]Harnik, V. and Makkai, M., A tree argument in infinitary model theory, Proceedings of the American Mathematical Society, vol. 67 (1977), pp. 309–313.CrossRefGoogle Scholar
[HMS]Harrington, L., Makkai, M. and Shelah, S., A proof of Vaught's conjecture for ω-stable theories, Israel Journal of Mathematics, vol. 49 (1984), pp. 259–280.Google Scholar
[L]Lascar, D., Le problème de la classification des modèles dénombrables, Publication des Groupes de Contact, Fonds National de la Recherche Scientifique, Sciences Mathématiques, Bruxelles, 1981, pp. 45–49.Google Scholar
[M1]Makkai, M., An “admissible” generalization of a theorem on countable sets of reals with applications, Annals of Mathematical Logic, vol. 11 (1970), pp. 1–30.CrossRefGoogle Scholar
[M2]Makkai, M., An example concerning Scott height, this Journal, vol. 46 (1981), pp. 301–318.Google Scholar
[Mo]Morley, M., The number of countable models, this Journal, vol. 35 (1970), pp. 14–18.Google Scholar
[N]Nadel, M., Scott sentences and admissible sets, Annals of Mathematical Logic, vol. 7 (1974), pp. 267–294.CrossRefGoogle Scholar
[R]Rubin, M., Theories of linear orders, Israel Journal of Mathematics, vol. 17 (1974), pp. 392–443.CrossRefGoogle Scholar
[Sa]Sacks, G., On the number of countable models, Southeast Asian Conference on Logic (Singapore, 1981, Chong, C. T. and Wicks, M. J., editors), North-Holland, Amsterdam, 1983, pp. 185–195.CrossRefGoogle Scholar
[Se]Scott, D., Logic with denumerably long formulas and finite strings of quantifiers, The theory of models (Addison, J. W., Henkin, L. and Tarski, A., editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
[Sh1]Shelah, S., Classification theory and the number of nonisomorphic models, North-Holland, Amsterdam, 1978.Google Scholar
[Sh2]Shelah, S., The spectrum problem I: ℵε-saturated models, the main gap, Israel Journal of Mathematics, vol. 43 (1982), pp. 324–356.CrossRefGoogle Scholar
[Sh3]Shelah, S., New edition of [Sh1] (to appear).Google Scholar
[St]Steel, J., On Vaught's conjecture, Cabal Seminar 76–77 (Kechris, A. S. and Moschovakis, Y. N., editors), Lecture Notes in Mathematics, vol. 689, Springer-Verlag, Berlin and New York, 1978, pp. 193– 208.CrossRefGoogle Scholar
[V]Vaught, R. L., Denumerable models of complete theories, Infinitistic methods (Proceedings of the symposium on the foundations of mathematics, Warsaw, 1959), Państwowe Wydawnictwo Naukowe, Warsaw, and Pergamon Press, Oxford and New York, 1961, pp. 303–321.Google Scholar