No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
There has been much work in developing the interconnections between model theory and algebra. Here we look at a particular example, the divisible ordered abelian groups, and show how the indiscernibles are related to the algebraic structure. Now a divisible ordered abelian group is a model of Th (Q, +, 0, <) and so is linearly ordered by <. Thus the theory is unstable and has a large number of models. It is therefore unrealistic to expect that a simple condition will completely determine a model. Instead we would just like to obtain nice algebraic invariants.
Definition. A subset C of a divisible ordered abelian group 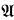 is a set of (order) indiscernibles iff for every sequence of integers n1,…,nk and for every c1 < … < ck and d1 < … < dk in C
is a set of (order) indiscernibles iff for every sequence of integers n1,…,nk and for every c1 < … < ck and d1 < … < dk in C
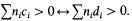
Note that this simplified form of indiscernibility is an immediate consequence of quantifier elimination for the theory. The above definition could be formulated in the language of +, 0, < but we have used subtraction as a matter of convenience. Similarly we may also use rational coefficients. Also note that a set of order indiscernibles is usually defined with respect to some external order. But in this case there are only two possibilities: the ordering inherited from 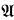 or its reverse. So we will always assume that a set of order indiscernibles has the ordering inherited from
or its reverse. So we will always assume that a set of order indiscernibles has the ordering inherited from 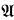 . We may sometimes refer to a set of indiscernibles as a sequence of indiscernibles if we want to explicitly mention the ordering associated with the set.
. We may sometimes refer to a set of indiscernibles as a sequence of indiscernibles if we want to explicitly mention the ordering associated with the set.
The results in this paper primarily come from a chapter in the author's Ph.D. thesis [6] which was written with the valuable guidance of Professor H. J. Keisler.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.