Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-16T13:14:51.844Z Has data issue: false hasContentIssue false
  • English
  • Français

On the structure of Ext(A,Z) in ZFC+

Published online by Cambridge University Press:  12 March 2014

G. Sageev  and
S. Shelah
G. Sageev
Affiliation:
Department of Mathematics, State University of New York at Buffalo, Buffalo, New York 14214-3093
S. Shelah
Affiliation:
Institute of Mathematics, The Hebrew University, Jerusalem, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

A fundamental problem in the theory of abelian groups is to determine the structure of Ext(A, Z) for arbitrary abelian groups A. This problem was raised by L. Fuchs in 1958, and since then has been the center of considerable activity and progress.

We briefly summarize the present state of this problem. It is a well-known fact that

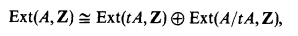
where tA denotes the torsion subgroup of A. Thus the structure problem for Ext(A, Z) breakdown to the two distinct cases, torsion and torsion free groups. For a torsion group T,

which is compact and reduced, and its structure is known explicitly [12].

For torsion free A, Ext(A, Z) is divisible; hence it has a unique representation

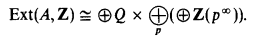
Thus Ext(A, Z) is characterized by countably many cardinal numbers, which we denote as follows: ν0(A) is the rank of the torsion free part of Ext(A, Z), and νp(A) are the ranks of the p-primary parts of Ext(A, Z), Extp(A, Z).

If A is free it is an elementary fact that Ext(A, Z) = 0. The second named author has shown [16] that in the presence of V = L the converse is also true. For countable torsion free, nonfree A, C. Jensen [13] has shown that νp(A) is either finite or and νp(A) ≤ ν0(A). Therefore, the case for uncountable, nonfree, torsion free groups A remains to be studied.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 2 , June 1985 , pp. 302 - 315
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chase, S., Function topologies on abelian groups, Illinois Journal of Mathematics, vol. 7 (1963), pp. 593–608.CrossRefGoogle Scholar
[2]Eklof, P., Whitehead's problem is undecidable, American Mathematical Monthly, vol. 83 (1976), pp. 775–788.CrossRefGoogle Scholar
[3]Eklof, P., Methods of logic in abelian group theory, Abelian group theory (Proceedings, Las Cruces, 1976), Lecture Notes in Mathematics, vol. 616, Springer-Verlag, Berlin, 1977, pp. 251–269.CrossRefGoogle Scholar
[4]Eklof, P. and Huber, M., Abelian group extensions and the axiom of constructibility, Commentarii Mathematici Hehetici, vol. 54 (1979), pp. 440–457.CrossRefGoogle Scholar
[5]Eklof, P., On the p-ranks of Ext(A,G), assuming CH, Abelian group theory (Proceedings, Oberwolfach, 1981), Lecture Notes in Mathematics, vol. 874, Springer-Verlag, Berlin, 1981, pp. 93–108.CrossRefGoogle Scholar
[6]Fuchs, L., Infinite abelian groups. Vol. I, Academic Press, New York, 1970.Google Scholar
[7]Fuchs, L., Infinite abelian groups. Vol. II, Academic Press, New York, 1973.Google Scholar
[8]Hiller, H., Huber, M. and Shelah, S., The structure of Uxt(A, Z) and V = L, Mathematische Zeitschrift, vol. 162 (1978), pp. 39–50.CrossRefGoogle Scholar
[9]Hiller, H. and Shelah, S., Singular cohomology in L, Israel Journal of Mathematics, vol. 28 (1977), pp. 313–319.CrossRefGoogle Scholar
[10]Huber, M., Caractérisation des groupes abéliens libres, et cardinalités, Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences, Séries A et B, vol. 285 (1977), pp. A1–A2.Google Scholar
[11]Hulanicki, A., Algebraic characterization of abelian divisible groups which admit compact topologies, Fundamenta Mat hernaticae, vol. 44 (1957), pp. 192–197.CrossRefGoogle Scholar
[12]Hulanicki, A., Algebraic structure of compact abelian groups, Bulletin de l'Académie Polonaise des Sciences, Séries des Sciences Mathématiques, Astronomiques et Physiques, vol. 6 (1958), pp. 71–73.Google Scholar
[13]Jensen, C., Les foncteurs dérivés de lim leurs applications en théorie des modules, Lecture Notes in Mathematics, vol. 254, Springer-Verlag, Berlin, 1972.Google Scholar
[14]Sageev, G. and Shelah, S., On the structure of Ext(A,Z) in L, manuscript, 1980.Google Scholar
[15]Sageev, G., Weak compactness and the structure of Ext(G, Z) in L, Abelian group theory ( Proceedings, Oberwolf ach, 1981), Lecture Notes in Mathematics, vol. 874, Springer-Verlag, Berlin, 1981, pp. 87–92.CrossRefGoogle Scholar
[16]Shelah, S., Infinite abelian groups—Whitehead problem and some constructions, Israel Journal of Mathematics, vol. 18 (1974), pp. 243–256.CrossRefGoogle Scholar
[17]Shelah, S., Whitehead groups may not be free, even assuming CH. I, Israel Journal of Mathematics, vol. 28 (1977), pp. 193–204.CrossRefGoogle Scholar
[18]Shelah, S., On the structure of Ext(G,Z) assuming V = L, manuscript, 1978.Google Scholar
[19]Shelah, S., Whitehead groups may not be free, even assuming CH. II, Israel Journal of Mathematics, vol. 35 (1980), pp. 257–285.CrossRefGoogle Scholar
[20]Shelah, S., On uncountable abelian groups, Israel Journal of Mathematics, vol. 32 (1979), pp. 311–330.CrossRefGoogle Scholar
[21]Shelah, S., Consistency of Ext(G,Z) = Q, Israel Journal of Mathematics, vol. 39 (1981), pp. 74–82.CrossRefGoogle Scholar