Published online by Cambridge University Press: 12 March 2014
In this paper, we prove a result that J. Y. Girard has conjectured for the last few years. That is,
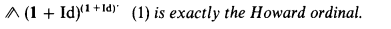
This result is part of a study of ordinal notations. For the proof, we use some concepts introduced in Parts I, II and III of this article (see [GV1], [GV2] and [V]); in particular, in Part III (see [V]) we defined the category GAR of gardens (of type Ω), and we have shown that there is an isomorphism between GAR and the category DIL Ω of dilators which send Ω into Ω. To describe this isomorphism, we defined a functor SYN from GAR to DIL Ω and a functor DEC from DIL Ω to GAR which are inverse to each other. The functor SYN is constructed by induction on the height x of the garden Jx, iterating, at each step of cofinality Ω, the operation UN (unification of variables; see [G1, Chapter 3]). Here, we define the functor S⊿ from GAR to DIL Ω: this construction is very close to that of SYN, but we iterate, at each step of cofinality Ω, the operation ⊿ (identification of variables; see [G, Chapter 3]). Technically, the definition of S⊿ is easier and more natural than that of SYN (as ⊿ is easier than UN) but is not inversible (as ⊿); for example, if we consider the (regular) garden GεΩ+1 introduced in [GV2],S⊿(GεΩ+1) is exactly the dilator N = ⋃0<n<ωNn, with N1 = 2 + Id, and 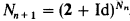 , but we are incapable of expressing SYN(GεΩ+1).
, but we are incapable of expressing SYN(GεΩ+1).
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.