Published online by Cambridge University Press: 12 March 2014
When dealing with axiomatic theories from a recursion-theoretic point of view, the notion of r.e. preordering naturally arises. We agree that an r.e. preorder is a pair 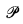 = 〈P, ≤P〉 such that P is an r.e. subset of the set of natural numbers (denoted by ω), ≤P is a preordering on P and the set {〈;x, y〉: x ≤Py} is r.e.. Indeed, if
= 〈P, ≤P〉 such that P is an r.e. subset of the set of natural numbers (denoted by ω), ≤P is a preordering on P and the set {〈;x, y〉: x ≤Py} is r.e.. Indeed, if 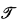 is an axiomatic theory, the provable implication of
is an axiomatic theory, the provable implication of 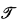 yields a preordering on the class of (Gödel numbers of) formulas of
yields a preordering on the class of (Gödel numbers of) formulas of 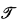 .
.
Of course, if ≤P is a preordering on P, then it yields an equivalence relation ~P on P, by simply letting x ~Py iff x ≤Py and y ≤Px. Hence, in the case of P = ω, any preordering yields an equivalence relation on ω and consequently a numeration in the sense of [4]. It is also clear that any equivalence relation on ω (hence any numeration) can be regarded as a preordering on ω. In view of this connection, we sometimes apply to the theory of preorders some of the concepts from the theory of numerations (see also Eršov [6]).
Our main concern will be in applications of these concepts to logic, in particular as regards sufficiently strong axiomatic theories (essentially the ones in which recursive functions are representable). From this point of view it seems to be of some interest to study some remarkable prelattices and Boolean prealgebras which arise from such theories. It turns out that these structures enjoy some rather surprising lattice-theoretic and universal recursion-theoretic properties.
After making our main definitions in §1, we examine universal recursion-theoretic properties of some r.e. prelattices in §2.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.