We consider the language L(Q), where L is a countable first-order language and Q is an additional generalized quantifier. A weak model for L(Q) is a pair 〈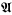, q〉 where 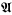is a first-order structure for L and q is a family of subsets of its universe. In case that q is the set of classes of some equivalence relation the weak model 〈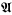, q〉 is called a partition model. The interpretation of Q in partition models was studied by Szczerba [3], who was inspired by Pawlak's paper [2]. The corresponding set of tautologies in L(Q) is called rough logic. In the following we will give a set of axioms of rough logic and prove its completeness. Rough logic is designed for creating partition models.

The partition models are the weak models arising from equivalence relations. For the basic properties of the logic of weak models the reader is referred to Keisler's paper [1]. In a weak model 〈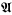, q〉 the formulas of L(Q) are interpreted as usual with the additional clause for the quantifier Q: 〈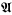, q〉 ⊨ Qx φ(x) iff there is some X ∊ q such that 〈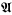, q〉 ⊨ φ(a) for all a ∊ X.

In case X satisfies the right side of the above equivalence we say that X is contained in φ(x) or, equivalently, φ(x) contains X.