Recursion categories have been proposed by Di Paola and Heller in [DPH] as the basis for a category-theoretic approach to recursion theory, in the context of a more general and ambitious project of a purely algebraic treatment of incompleteness phenomena. The way in which the classical notion of creative set is rendered in this new category-theoretic framework plays, therefore, a central role. This is done in [DPH] (Definition 8.1) by defining the notion of creative domains or, rather, domains which are creative relative to some criterion: thus, in a recursion category, every criterion provides a notion of creativeness.

A basic result on creative domains (cf. [DPH, Theorem 8.13]) is that, under certain assumptions, a version of the classical result, due to Myhill [MYH], stating that every creative set is complete, holds: in a recursion category with equality (i.e. 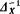exists for every object X) and having enough atoms, every domain which is creative with respect to atoms is also complete.