Article contents
On analytic filters and prefilters
Published online by Cambridge University Press: 12 March 2014
Abstract
We show that every analytic filter is generated by a 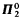 prefilter, every
prefilter, every 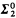 filter is generated by a
filter is generated by a 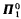 prefilter, and if
prefilter, and if 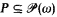 is a
is a 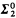 prefilter then the filter generated by it is also
prefilter then the filter generated by it is also 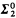 . The last result is unique for the Borel classes, as there is a
. The last result is unique for the Borel classes, as there is a 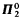 -complete prefilter P such that the filter generated by it is
-complete prefilter P such that the filter generated by it is 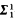 -complete. Also, no complete coanalytic filter is generated by an analytic prefilter. The proofs use König's infinity lemma, a normal form theorem for monotone analytic sets, and Wadge reductions.
-complete. Also, no complete coanalytic filter is generated by an analytic prefilter. The proofs use König's infinity lemma, a normal form theorem for monotone analytic sets, and Wadge reductions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
REFERENCES
- 3
- Cited by


