Published online by Cambridge University Press: 12 March 2014
Let σ(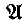 ) denote the number of automorphisms of a model
) denote the number of automorphisms of a model 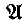 of power ω1. We derive a necessary and sufficient condition in terms of trees for the existence of an
of power ω1. We derive a necessary and sufficient condition in terms of trees for the existence of an 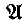 with
with 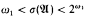 . We study the sufficiency of some conditions for
. We study the sufficiency of some conditions for 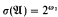 . These conditions are analogous to conditions studied by D. Kueker in connection with countable models.
. These conditions are analogous to conditions studied by D. Kueker in connection with countable models.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.