In 1960 G. F. Rose [R] made the following definition: A function f: ω → ω is (m, n)-computable, where 1 ≤ m ≤ n, iff there exists a recursive function R: ωn → ωn such that, for all n-tuples (x1,…, xn) of distinct natural numbers,

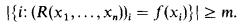
J. Myhill (see [McN, p. 393]) asked if f had to be recursive if m was close to n; B. A. Trakhtenbrot [T] responded by showing in 1963 that f is recursive whenever 2m > n. This result is optimal, because, for example, the characteristic function of any semirecursive set is (1,2)-computable. Trakhtenbrot's work was extended by E. B. Kinber [Ki1], using similar techniques. In 1986 R. Beigel [B] made a powerful conjecture, much more general than the above results. Partial verification, falling short of a full proof, appeared in [O]. Using new techniques, M. Kummer has recently established the conjecture, which will henceforth be referred to as the cardinality theorem (CT). It is the goal of this paper to show the connections between these various theorems, to review the methods used by Trakhtenbrot, and to use them to prove a special case of CT strong enough to imply Kinber's theorem (see §3). We thus have a hierarchy of results, with CT at the top. We will also include a discussion of Kummer's methods, but not a proof of CT.