No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
Suppose λ is a singular cardinal of uncountable cofinality κ. For a model 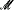 of cardinality λ, let No(
of cardinality λ, let No(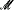 ) denote the number of isomorphism types of models
) denote the number of isomorphism types of models 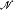 of cardinality λ which are L∞λ-equivalent to
of cardinality λ which are L∞λ-equivalent to 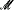 . In [7] Shelah considered inverse κ-systems
. In [7] Shelah considered inverse κ-systems  of abelian groups and their certain kind of quotient limits Gr(
of abelian groups and their certain kind of quotient limits Gr( )/ Fact(
)/ Fact( ). In particular Shelah proved in [7, Fact 3.10] that for every cardinal Μ there exists an inverse κ-system
). In particular Shelah proved in [7, Fact 3.10] that for every cardinal Μ there exists an inverse κ-system  such that
such that  consists of abelian groups having cardinality at most Μκ and card(Gr(
consists of abelian groups having cardinality at most Μκ and card(Gr( )/ Fact(
)/ Fact( )) = Μ. Later in [8, Theorem 3.3] Shelah showed a strict connection between inverse κ-systems and possible values of No (under the assumption that θκ < λ for every θ < λ): if
)) = Μ. Later in [8, Theorem 3.3] Shelah showed a strict connection between inverse κ-systems and possible values of No (under the assumption that θκ < λ for every θ < λ): if  is an inverse κ-system of abelian groups having cardinality < λ, then there is a model
is an inverse κ-system of abelian groups having cardinality < λ, then there is a model 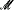 such that card(
such that card(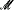 ) = λ and No(
) = λ and No(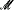 ) = card(Gr(
) = card(Gr( )/ Fact(
)/ Fact( )). The following was an immediate consequence (when θκ < λ for every θ < λ): for every nonzero Μ < λ or Μ = λκ there is a model
)). The following was an immediate consequence (when θκ < λ for every θ < λ): for every nonzero Μ < λ or Μ = λκ there is a model 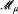 , of cardinality λ with No(
, of cardinality λ with No(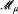 ) = Μ. In this paper we show: for every nonzero Μ ≤ λκ there is an inverse κ-system
) = Μ. In this paper we show: for every nonzero Μ ≤ λκ there is an inverse κ-system  of abelian groups having cardinality < λ such that card(Gr(
of abelian groups having cardinality < λ such that card(Gr( )/ Fact(
)/ Fact( )) = Μ (under the assumptions 2κ < λ and θ<κ < λ for all θ < λ when Μ > λ), with the obvious new consequence concerning the possible value of No. Specifically, the case No(
)) = Μ (under the assumptions 2κ < λ and θ<κ < λ for all θ < λ when Μ > λ), with the obvious new consequence concerning the possible value of No. Specifically, the case No(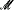 ) = λ is possible when θκ > λ for every λ < λ.
) = λ is possible when θκ > λ for every λ < λ.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.