Published online by Cambridge University Press: 12 March 2014
Hybrid languages are expansions of propositional modal languages which can refer to (or even quantify over) worlds. The use of strong hybrid languages dates back to at least [Pri67], but recent work (for example [BS98, BT98a, BT99]) has focussed on a more constrained system called H(↓, @). We show in detail that 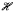 (↓, @) is modally natural. We begin by studying its expressivity, and provide model theoretic characterizations (via a restricted notion of Ehrenfeucht-Fraïssé game, and an enriched notion of bisimulation) and a syntactic characterization (in terms of bounded formulas). The key result to emerge is that
(↓, @) is modally natural. We begin by studying its expressivity, and provide model theoretic characterizations (via a restricted notion of Ehrenfeucht-Fraïssé game, and an enriched notion of bisimulation) and a syntactic characterization (in terms of bounded formulas). The key result to emerge is that 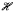 (↓, @) corresponds to the fragment of first-order logic which is invariant for generated submodels. We then show that
(↓, @) corresponds to the fragment of first-order logic which is invariant for generated submodels. We then show that 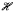 (↓, @) enjoys (strong) interpolation, provide counterexamples for its finite variable fragments, and show that weak interpolation holds for the sublanguage
(↓, @) enjoys (strong) interpolation, provide counterexamples for its finite variable fragments, and show that weak interpolation holds for the sublanguage 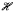 (@). Finally, we provide complexity results for
(@). Finally, we provide complexity results for 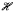 (@) and other fragments and variants, and sharpen known undecidability results for
(@) and other fragments and variants, and sharpen known undecidability results for 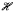 (↓, @).
(↓, @).
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.