Published online by Cambridge University Press: 12 March 2014
Let ℒ be the set of all formulas of a given first order predicate logic (with or without identity). For each positive integer n, let ℒn be the set of all formulas φ in ℒ logically equivalent to a formula of the form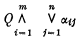
where Q is a (possibly empty) string of quantifiers, m is a positive integer, and each αij is either an atomic formula or the negation of an atomic formula.
The work of the first named author was supported by a research grant from the National Science Foundation. The work of the second named author was supported by a National Science Foundation Cooperative Fellowship.
2 Before arriving at the final result, the bound on the length of the disjunctions in the improved normal form took, with the passage of time, the following values (in the opinion of the authors): 3·p + 2p, 4·p, 3·p + 2p, 5·p, 3·p, max(3, p), and finally, in the case of logic with identity, max (2, p). The authors became interested in this problem through their investigations on reduced products in the theory of models. Chronologically, the results of § 2 preceded those of § 1. In the light of the methods of § 1, the proofs in § 2 were considerably simplified.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.