Article contents
An Elementary Approach to the Fine Structure of L
Published online by Cambridge University Press: 15 January 2014
Extract
We present here an approach to the fine structure of L based solely on elementary model theoretic ideas, and illustrate its use in a proof of Global Square in L. We thereby avoid the Lévy hierarchy of formulas and the subtleties of master codes and projecta, introduced by Jensen [3] in the original form of the theory. Our theory could appropriately be called ”Hyperfine Structure Theory”, as we make use of a hierarchy of structures and hull operations which refines the traditional Lα -or Jα-sequences with their Σn-hull operations.
§1. Introduction. In 1938, K. Gödel defined the model L of set theory to show the relative consistency of Cantor's Continuum Hypothesis. L is defined as a union
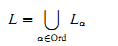
of initial segments which satisfy: L0 = ∅, Lλ = ∪α<λLα for limit ordinals λ, and, crucially, Lα + 1 = the collection of 1st order definable subsets of Lα. Since every transitive model of set theory must be closed under 1st order definability, L turns out to be the smallest inner model of set theory. Thus it occupies the central place in the set theoretic spectrum of models.
The proof of the continuum hypothesis in L is based on the very uniform hierarchical definition of the L-hierarchy. The Condensation Lemma states that if π : M → Lα is an elementary embedding, M transitive, then 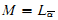 some
some 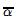 ; the lemma can be proved by induction on α. If a real, i.e., a subset of ω, is definable over some Lα,then by a Löwenheim-Skolem argument it is definable over some countable M as above, and hence over some
; the lemma can be proved by induction on α. If a real, i.e., a subset of ω, is definable over some Lα,then by a Löwenheim-Skolem argument it is definable over some countable M as above, and hence over some 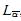 ,
, 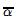 < ω1. This allows one to list the reals in L in length ω1 and therefore proves the Continuum Hypothesis in L.
< ω1. This allows one to list the reals in L in length ω1 and therefore proves the Continuum Hypothesis in L.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 10
- Cited by


