Skip to main content
SpringerLink
Log in

The Branch-and-Bound Algorithm for the Traveling Salesman Problem is Not a Direct Algorithm

  • Published:
Automatic Control and Computer Sciences Aims and scope Submit manuscript

Abstract—

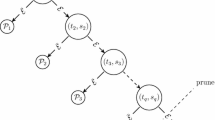
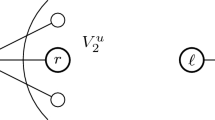
This article considers the concept of a linear separation direct algorithm introduced by V.A. Bondarenko in 1983. The concept of a direct algorithm is defined using the solution graph of a combinatorial optimization problem. The vertices of this graph are all feasible solutions of the problem. Two solutions are called adjacent if there are input data for which these and only these solutions are optimal. A key feature of direct algorithms is that their complexity is bounded from below by the clique number of the solution graph. In 2015–2018, there were five articles published, the main results of which are estimates of the clique numbers of polyhedron graphs associated with various combinatorial optimization problems. The thesis that the class of direct algorithms is broad and includes many classical combinatorial algorithms, including the branch-and-bound algorithm for the traveling salesman problem proposed by J.D.C. Little, K.G. Murty, D.W. Sweeney, and C. Karel in 1963, was the main motivation for these articles. We show that this algorithm is not a direct algorithm. Earlier, in 2014, the author of this article showed that the Hungarian algorithm for the assignment problem is not a direct algorithm. Therefore, the class of direct algorithms is not as broad as previously assumed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.

Similar content being viewed by others

Notes

  1. But no source references with corresponding proofs were given.

  2. Elements of the matrix can always be written out in a row or a column.

REFERENCES

  1. Bondarenko, V., Nikolaev, A., and Shovgenov, D., 1-skeletons of the spanning tree problems with additional constraints, Autom. Control Comput. Sci., 2017, vol. 51, no. 7, pp. 682–688.  https://doi.org/10.3103/S0146411617070033

    Article  Google Scholar 

  2. Bondarenko, V. and Nikolaev, A., On graphs of the cone decompositions for the min-cut and max-cut problems, Int. J. Math. Math. Sci., 2016, vol. 2016, p. 7863650.  https://doi.org/10.1155/2016/7863650

    Article  MathSciNet  MATH  Google Scholar 

  3. Bondarenko, V. and Nikolaev, A., Some properties of the skeleton of the pyramidal tours polytope, Electron. Notes Discrete Math., 2017, vol. 61, pp. 131–137.  https://doi.org/10.1016/j.endm.2017.06.030

    Article  MATH  Google Scholar 

  4. Bondarenko, V.A., Nikolaev, A.V., and Shovgenov, D.A., Polyhedral characteristics of balanced and unbalanced bipartite subgraph problems, Autom. Control Comput. Sci., 2017, vol. 51, no. 7, pp. 576–585.  https://doi.org/10.3103/S0146411617070276

    Article  Google Scholar 

  5. Bondarenko, V.A. and Nikolaev, A.V., On the skeleton of the polytope of pyramidal tours, J. Appl. Ind. Math., 2018, vol. 12, no. 1, pp. 9–18.  https://doi.org/10.1134/S1990478918010027

    Article  MathSciNet  MATH  Google Scholar 

  6. Bondarenko, V.A., Nonpolynomial lowerbound of the traveling salesman problem complexity in one class of algorithms, Autom. Remote Control, 1983, vol. 44, no. 9, pp. 1137–1142.

    MATH  Google Scholar 

  7. Bondarenko, V., Geometrical methods of systems analysis in combinatorial optimization, Doctor Sci. (Phys.-Math.) Dissertation, Yaroslavl’: Demidov Yaroslavl State Univ., 1993.

  8. Bondarenko, V. and Maksimenko, A., Geometricheskie konstruktsii i slozhnost’ v kombinatornoi optimizatsii (Geometric Structures and Complexity in Combinatorial Optimization), Moscow: URSS, 2008.

  9. Maksimenko, A.N., Characteristics of complexity: clique number of a polytope graph and rectangle covering number, Mod. Anal. Inf. Sist., 2014, vol. 21, no. 5, pp. 116–130.

    Article  Google Scholar 

  10. Little, J.D.C., Murty, K.G., Sweeney, D.W., and Karel, C., An algorithm for the traveling salesman problem, Oper. Res., 1963, vol. 11, no. 6, pp. 972–989.

    Article  Google Scholar 

  11. Reingold, E., Nievergelt, J., and Deo, N., Combinatorial Algorithms: Theory and Practice, Prentice Hall College Div., 1977.

    MATH  Google Scholar 

  12. Padberg, M.W. and Rao, M.R., The travelling salesman problem and a class of polyhedra of diameter two, Math. Program., 1974, vol. 7, no. 1, pp. 32–45.  https://doi.org/10.1007/BF01585502

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Demidov Yaroslavl State University, 150003, Yaroslavl, Russia

    A. N. Maksimenko

Authors
  1. A. N. Maksimenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. N. Maksimenko.

Ethics declarations

The author declares that he has no conflicts of interest.

Additional information

Translated by O. Pismenov

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maksimenko, A.N. The Branch-and-Bound Algorithm for the Traveling Salesman Problem is Not a Direct Algorithm. Aut. Control Comp. Sci. 55, 816–826 (2021). https://doi.org/10.3103/S0146411621070269

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0146411621070269

Keywords:

Search

Navigation