Parameter Estimation and Its Application on Designing Adaptive Nonlinear Model Based Control Schemes for the Time Varying System

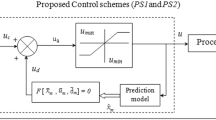
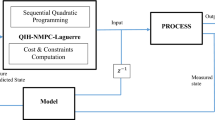
Abstract

This work deals with implementation of adaptive nonlinear model-based control (NMBC) scheme on the time varying system. In this approach, only influential model parameter was estimated using well recognized parameter estimation techniques and predicted value of the parameters were used to synthesize the control law. Detailed guidelines on tuning controller parameters were discussed in this paper. In order to demonstrate the practical utility and usefulness of the NMBC control framework, a typical nonlinear industrial process was chosen. The realistic simulations like servo-regulatory compliance, elimination of measurement noise with a state-of-the-art simulator ensures the efficacy of the proposed controller. The performance assessment of the NMBC schemes (computational speed, mean square error (MSE)) were analyzed and compared with the traditional adaptive PI (TA-PI) control strategy. Furthermore, the convergence assessing chart (mean square deviation (MSD)) for different estimators were compared in order to analyze the merits and demerits associated with them. From the extensive simulation studies, robustness features of the aforementioned control schemes have been investigated.

APPENDIX

1.1 APPENDIX A. CONTINUOUS-TIME PARAMETER FILTER USING EKF ESTIMATION SCHEME

Initialization of the filter [18, 19]:

$${\mathbf{\hat {\Theta }}}_{0}^{a} = E[{\mathbf{\Theta }}_{0}^{a}],$$

(A.1)

$${{{\mathbf{P}}}_{{{{\Theta }_{0}}}}} = E[({\mathbf{\Theta }}_{0}^{a} - {\mathbf{\hat {\Theta }}}_{0}^{a}){{({\mathbf{\Theta }}_{0}^{a} - {\mathbf{\hat {\Theta }}}_{0}^{a})}^{{\text{T}}}}].$$

(A.2)

Time update equations:

$${{{\mathbf{\hat {\Theta }}}}^{f}}(t) = {{{\mathbf{\hat {\Theta }}}}^{a}}(t - 1),$$

(A.3)

$${\mathbf{P}}_{\Theta }^{f}(t) = {{{\mathbf{P}}}_{\Theta }}(t - 1) + {\mathbf{Q}}.$$

(A.4)

Computation of Kalman gain:

$${{{\mathbf{K}}}_{{{\text{EKF}},\Theta }}} = {\mathbf{P}}_{\Theta }^{f}(t){\mathbf{J}}_{\Theta }^{{\text{T}}}{{({{{\mathbf{J}}}_{\Theta }}{\mathbf{P}}_{\Theta }^{f}(t){\mathbf{J}}_{\Theta }^{{\text{T}}} + {\mathbf{R}})}^{{ - 1}}},$$

(A.5)

${{{\mathbf{J}}}_{\Theta }}$ is the Jacobian of the observation matrix and can be expressed as

$${{{\mathbf{J}}}_{\Theta }} = {{\left. {\frac{{\partial h{{{({\mathbf{x}}(t - 1),{\mathbf{\Theta }})}}^{{\text{T}}}}}}{{\partial \Theta }}} \right|}_{{(\Theta = {{{\hat {\Theta }}}^{f}}(t))}}}.$$

(A.6)

Hence, the measurement update equations are as follows:

$${{{\mathbf{\hat {\Theta }}}}^{a}}(t) = {{{\mathbf{\hat {\Theta }}}}^{f}}(t) + {{{\mathbf{K}}}_{{{\text{EKF}},\Theta }}}({\mathbf{pv}} - h({\mathbf{x}}(t - 1),{{{\mathbf{\hat {\Theta }}}}^{f}}(t))),$$

(A.7)

$${\mathbf{P}}_{\Theta }^{a}(t) = ({\mathbf{I}} - {{{\mathbf{K}}}_{{{\text{EKF}},\Theta }}}{{{\mathbf{J}}}_{\Theta }}){\mathbf{P}}_{\Theta }^{f}(t),$$

(A.8)

1.2 APPENDIX B. CONTINUOUS-TIME PARAMETER FILTER USING USING UKF ESTIMATION LAW

Let us skip the filter initialization and time update equations (mentioned in Appendix A). A set of $(2L + 1)$ sigma points with the associated weights $w(i)$ are chosen symmetrically about ${{{\mathbf{\hat {\Theta }}}}^{f}}(t)$ as follows [20, 21, 25]:

$${{{\mathbf{\Theta }}}_{s}} = [{{{\mathbf{\hat {\Theta }}}}^{f}}(t){\text{ }}{{{\mathbf{\hat {\Theta }}}}^{f}}(t) + \sqrt {(L + \kappa ){\mathbf{P}}_{\Theta }^{f}(t)} {\text{ }}{{{\mathbf{\hat {\Theta }}}}^{f}}(t) - \sqrt {(L + \kappa ){\mathbf{P}}_{\Theta }^{f}(t)} ].$$

(B.1)

The measurement prediction $({\mathbf{\hat {p}v}}(t))$, computation of innovation $({\mathbf{e}}(t))$, covariance matrix of innovation $({{{\mathbf{P}}}_{{ee}}}(t))$, the cross-covariance matrix between the predicted process/controller parameter(s) estimation error and innovation $({{{\mathbf{P}}}_{{\theta e}}}(t))$ are computed as follows:

$${\mathbf{p}}{{{\mathbf{v}}}_{\Theta }}(t) = h({\mathbf{\hat {g}}}(t - 1),{{{\mathbf{\Theta }}}_{s}}),$$

(B.2)

$${\mathbf{\hat {p}v}}(t) = \sum\limits_0^{2L} {w_{i}^{m}{\mathbf{p}}{{{\mathbf{v}}}_{\Theta }}(t)} ,$$

(B.3)

$${\mathbf{e}}(t) = {\mathbf{pv}}(t) - {\mathbf{\hat {p}v}}(t),$$

(B.4)

$${{{\mathbf{P}}}_{{ee}}}(t) = \sum\limits_{i = 0}^{2L} {w_{i}^{c}({\mathbf{pv}}_{\Theta }^{i}(t) - {\mathbf{\hat {p}v}}(t)} ){{({\mathbf{pv}}_{\Theta }^{i}(t) - {\mathbf{\hat {p}v}}(t))}^{{\text{T}}}} + {\mathbf{R}},$$

(B.5)

$${{{\mathbf{P}}}_{{\theta e}}}(t) = \sum\limits_{i = 0}^{2L} {w_{i}^{c}({\mathbf{\hat {\Theta }}}_{s}^{i}(t) - {{{{\mathbf{\hat {\Theta }}}}}^{f}}(t))} ({{({\mathbf{pv}}_{\Theta }^{i}(t) - {\mathbf{\hat {p}v}}(t))}^{{\text{T}}}},$$

(B.6)

where ${{w}_{0}} = {\kappa \mathord{\left/ {\vphantom {\kappa {(L + \kappa )}}} \right. \kern-0em} {(L + \kappa )}}$ and ${{w}_{i}} = \kappa {\text{/}}(2(L + \kappa ))$. The Kalman gain is computed as

$${{{\mathbf{K}}}_{{{\text{UKF}},{\mathbf{\Theta }}}}} = {{{\mathbf{P}}}_{{\theta e}}}({\mathbf{P}}_{{ee}}^{{ - 1}}).$$

(B.7)

Hence, the measurement update equations are as follows:

$${{{\mathbf{\hat {\Theta }}}}^{a}}(t) = {{{\mathbf{\hat {\Theta }}}}^{f}}(t) + {{{\mathbf{K}}}_{{{\text{UKF}},{\mathbf{\Theta }}}}}{\mathbf{e}}(t),$$

(B.8)

$${\mathbf{P}}_{{\mathbf{\Theta }}}^{a} = {\mathbf{P}}_{{\mathbf{\Theta }}}^{f} - {{{\mathbf{K}}}_{{{\text{UKF}},{\mathbf{\Theta }}}}}{{{\mathbf{P}}}_{{ee}}}{\mathbf{K}}_{{{\text{UKF}},{\mathbf{\Theta }}}}^{{\text{T}}}.$$

(B.9)

1.3 APPENDIX C. CONTINUOUS-TIME EnKF FILTER DERIVED FROM EKF ESTIMATION SCHEME

Let’s assume, ${{{\mathbf{\bar {\Theta }}}}^{f}}$ and ${{{\mathbf{\bar {\Theta }}}}^{a}}$ represent forecast and posterior ensemble mean of the estimated parameter(s) ${{{\mathbf{\hat {\Theta }}}}^{f}}$ and ${{{\mathbf{\hat {\Theta }}}}^{a}}$ respectively whereas ${{{\mathbf{P}}}^{f}}$ and ${{{\mathbf{P}}}^{a}}$ corresponds to the covariance’s of the forecast and analysis respectively. Skipping the filter initialization (see Appendix A), time update equations can be written as [17, 19]:

$${{{\mathbf{\hat {\Theta }}}}^{f}}(t) = f({{{\mathbf{\hat {\Theta }}}}^{a}}(t - 1)) + w,$$

(C.1)

$${{{\mathbf{P}}}^{f}}{{H}^{{\text{T}}}} \equiv \frac{1}{{N - 1}}\sum\limits_{k = 1}^N {({{{{\mathbf{\hat {\Theta }}}}}^{f}} - \overline {{{{\mathbf{\Theta }}}^{f}}} )} {{(H{{{\mathbf{\hat {\Theta }}}}^{f}} - \overline {H{{{\mathbf{\Theta }}}^{f}}} )}^{{\text{T}}}},$$

(C.2)

$$H{{{\mathbf{P}}}^{f}}{{H}^{{\text{T}}}} \equiv \frac{1}{{N - 1}}\sum\limits_{k = 1}^N {(H{{{{\mathbf{\hat {\Theta }}}}}^{f}} - \overline {H{{{\mathbf{\Theta }}}^{f}}} )} {{(H{{{\mathbf{\hat {\Theta }}}}^{f}} - \overline {H{{{\mathbf{\Theta }}}^{f}}} )}^{{\text{T}}}},$$

(C.3)

$${{{\mathbf{K}}}_{{{\text{EnKF}},\Theta }}} = {{{\mathbf{P}}}^{f}}{{H}^{{\text{T}}}}{{(H{{{\mathbf{P}}}^{f}}{{H}^{{\text{T}}}} + {\mathbf{R}})}^{{ - 1}}},$$

(C.4)

$${\mathbf{p}}{{{\mathbf{v}}}_{i}}(t) = {\mathbf{pv}}(t) + {v},$$

(C.5)

$${{{\mathbf{\hat {\Theta }}}}^{a}}(t) = {{{\mathbf{\hat {\Theta }}}}^{f}}(t) + {{{\mathbf{K}}}_{{{\text{EnKF}},\Theta }}}({\mathbf{p}}{{{\mathbf{v}}}_{i}}(t) - H{{{\mathbf{\hat {\Theta }}}}^{a}}(t)).$$

(C.6)