1.
Introduction
1.1. Background
Inspired by the vigorous development of AI and big data technology in recent decades, researchers currently pay much attention to deriving partial differential equations (PDEs) based on neural networks combined with observation data. Earlier attempts on data-driven discovery of hidden physical laws include [1] and [2]. They used symbolic regression to learn multiple models from basic operators and operands to explain observed behavior and then chose the best model from candidate models by the advantage of new sets of initial conditions. In the more recent studies of [3,4,5], authors employed Gaussian process regression [6] to devise functional representations that are tailored to a given linear differential operator. They were able to accurately infer solutions and provide uncertainty estimates for several prototype problems in mathematical physics. However, local linearization of any nonlinear term in time and certain prior assumptions of the Bayesian nature of Gaussian process regression limit the representation capacity of the model. Other researchers represented by [7,8,9,10] have proposed an approach using sparse regression. They constructed a dictionary of simple functions and partial derivatives that were likely to appear in the unknown governing equations. Then, they took advantage of sparsity promoting techniques to select candidates that most accurately represent the data. Raissi et al., [11] introduced physics informed neural network (PINN) for solving two main classes of problems: data-driven solution and data-driven discovery of partial differential equations. They suggested that if the considered PDE is well-posed and its solution is unique, then the PINN method is capable of achieving good predictive accuracy given a sufficiently expressive neural network architecture and a sufficient number of collocation points. The method was explored for Schrödinger equation, Allen-Cahn equation, and Korteweg-de Vries (KdV) in one dimension (1D) and Navier-Stokes in two dimensions (2D). However, the neural network methods struggle in learning the nonlinear hyperbolic PDE that governs two-phase transport in porous media [12]. They experimentally indicate that this shortcoming of PINN for hyperbolic PDEs is not related to the specific architecture or to the choice of the hyperparameters but is related to the lack of regularity in the solution. Long et al., [13,14] proposed a combination of numerical approximation of differential operators by convolutions and a symbolic multi-layer neural network for model recovery. They used convolutions to approximate differential operators with properly constrained filters and to approximate the nonlinear response by deep neural networks. Models that are explored include Burgers equation
where the constant parameters λ1 and λ2 must be learned. Moreover, the advection-diffusion equation
was also considered. Herein, the parameter λ2 is known whereas k(x)=(a(x),b(x))⊤ is the unknown space-dependent coefficient to be learned. Furthermore, the diffusion-reaction problem given by Eq (1.3),
where g(u) is unknown and must be found by means of the observation data, was also successfully demonstrated.
In this work we focus on the problem of learning the unknown nonlinear flux function f(u) that is involved in the general scalar nonlinear conservation law, here restricted to the one-dimensional case, given by Eq (1.4)
where u=u(x,t) is the main variable. Burgers equation (1.1) amounts to the case with flux function f(u)=λ12u2 in Eq (1.4). Hence, the main challenge in Eq (1.4) is that the flux function f(u), which is a nonlinear function of u, itself is unknown and there is no viscous term in the form uxx that can regularize the solution.
1.2. Problem statement and novelty
The learning of the nonlinear flux function f(u) in Eq (1.4) involves several new aspects as compared to the other PDE models Eqs (1.1)–(1.2).
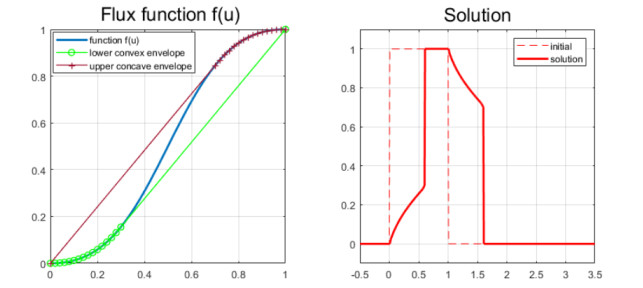
(i) Lack of observation data. It is well known that Eq (1.4) will generate shock wave solutions u(x,t) in finite time, i.e., solutions that contain one or sevel discontinuities expressed as a jump (uL,uR) with uL≠uR, despite the fact that initial data u0(x) is smooth [15,16]. In particular, the specific form of f(u) in the interval [min(uL,uR),max(uL,uR)] is not used in the construction of the entropy solution, only the slope s=f(uL)−f(uR)uL−uR. As jumps arise and disappear in the solution over the time period for which observation data is collected, the data may lack information about f(u). An illustration of this situation is given in Figure 1. In the left panel we plot the flux function f(u)=u2/(u2+(1−u)2). In the right panel the entropy solution after a time T=0.5 is shown. At time t=0, the initial data u0(x) involves one jump at x=0 and another jump at x=1. The initial jump at x=0 is instantly transformed into a solution that is a combination of a continuous wave solution (rarefaction wave) and a discontinuous wave (uL,uR)≈(0.3,1.0), as dictated by the lower convex envelope shown in the left panel (green curve) [15]. Similarly, the initial jump at x=1 is transformed into a solution that is a combination of a continuous wave solution (rarefaction wave) and a discontinuous wave (uL,uR)≈(0.7,0), in accordance with the upper concave envelope illustrated in left panel (brown curve) [15]. From this example, we see that we have no observation data that directly can reveal the shape of f(u) in the interval u∈[0.3,0.7] (approximately).
(ii) Lack of regularity. Previous work based on the PINN approaches mentioned above relies on imposing the structure of the underlying PDE model by including an error term in the loss function. This would amount to computing the left-hand-side of Eq (1.4). Due to the lack of regularity in the solution as illustrated by the example in Figure 1 (right panel), it seems not clear how to implement this in a PINN framework. We refer to [12] for investigations related to this point which found that it was necessary to consider the viscous approximation ut+f(u)x=εuxx with a small value ε>0 to learn the forward solution.
1.3. Our approach
Our aim is to learn the unknown nonlinear function f(u) from observation data in terms of solution behavior collected at different points (xj,ti) in space and time. The approach we explore in this work relies on the two following building blocks: (i) We represent the unknown function f(u) by a symbolic multi-layer neural network; (ii) Instead of including the form of the conservation law Eq (1.4) explicitly in the loss function as in PINN, we use a standard simple entropy-satifying discrete scheme associated with Eq (1.4) to account for this information during the learning process. The numerical scheme allows us to evolve the given initial data over the relevant time interval and collect predicted data which is accounted for in the loss function.
Regarding point (i), inspired by the symbolic neural network that is used in [17,18], we can learn an analytic expression that has a derivative similar to the true f′(u). The reason why it is attractive to learn the analytic expression is that, unlike black box learning, system identification has explanatory value. That is, once we have extracted an analytical expression of the hidden flux function f(u), e.g., based on data from a more or less complex system, the shape of the flux function provides precise insight into finer wave propagation mechanisms involved in the system under consideration. In particular, predictions can then be made for any other initial state. Our approach bears similarity to the underlying idea employed in the recent work [13,14]. However, an essential difference is that the flux function f(u)x cannot be expressed by f′(u)ux as f(u) is not in general a differentiable function in our problem. Therefore, we rely on using an entropy satifying discrete scheme, which is guaranteed to converge to the entropy solution of Eq (1.4) [15], to identify an analytical expression of the flux function f(u) which is present in the numerical scheme in the form of a symbolic neural network.
1.4. Related work
James and Sepúlveda formulated the inverse problem of flux identification as that of minimizing a suitable cost function [19]. Relying on the viscous approximation, it was shown that the perturbed problem converged to the original hyperbolic problem [19] by letting the viscous term vanish. Holden et al used the front-tracking algorithm to reconstruct the flux function from observed solutions to problems with suitable initial data [20]. Several recent studies have addressed the reconstruction of the flux function for sedimentation problems that involve the separation of a flocculated suspension into a clear fluid and a concentrated sediment [21,22]. In particular, Bürger and Diehl showed that the inverse problem of identifying the batch flux density function has a unique solution, and derived an explicit formula for the flux function [23]. This method was recently extended to construct almost the entire flux function [24] by using a cone-shaped separator. For another interesting example of the challenge of identification of the unknown flux function f(u), we refer to [25]. The author explored a direct inversion method based on using linear combinations of finite element hat functions to represent unknown nonlinear function f. Finally, for an example with neural networks used in combination with discrete schemes to optimize computations of a nonlinear conservation law, see [26].
The remainder of this paper is organized as follows: Section 2 gives a presentation of the approach that we explore. In Section 3 and Section 4 we conduct numerical studies where synthetic data has been generated from a general class of flux functions ranging from purely concave to highly non-convex functions. Concluding thoughts are given in Section 5.
2.
Framework
2.1. Nonlinear conservation laws and entropy satisfying solutions
It is well known that conservation laws of the form Eq (1.4) do not in generall possess classical solutions. Instead one must consider weak solutions in the sense that the following integral equality holds [15,27,28]
for all ϕ∈C1 such that ϕ(x,t):Ωx×(0,T)→R and which is compactly supported, i.e., ϕ vanishes at x→Ωx and t→T. It follows that if a discontinuity occurs in the solution, i.e., a left state uL and a right state uR, then it must propagate with the speed s given by [15,28]
This follows from mass conservation and, thus, must be satified across any discontinuity [15,28]. However, direct calculations show that there are several weak solutions for one and the same initial data [27]. To overcome this issue of non-uniqueness of weak solutions, we need criteria to determine whether a proposed weak solution is admissible or not. This has led to the class of entropy solutions, which amounts to introducing an additional constraint which ensures that the unique physically relevant one is found among all the possible weak solutions.
There are different ways to express the entropy condition for scalar nonlinear conservation laws. One variant is by introducing an entropy pair (η,q) where η:R→R is any strictly convex function and q:R→R is constructed as [28,29]
for any v. This implies that q′=f′η′. Then, u is an entropy solution of Eq (1.4) if (i) u is a weak solution in the sense of Eq (2.1); (ii) u satisfies in a weak sense η(u)t+q(u)x≤0 for any pair (η,q). This condition can also be formulated as the following characterization of a discontinuity (uL,uR) [28,30]: For all numbers v between uL and uR,
where s is given by Eq (2.2). This entropy condition can naturally be accounted for by introducing the upper concave envelope and lower convex envelope, as indicated in Figure 1 (left panel) [15,30]. In particular, it gives a tool for constructing exact solutions.
From this characterization of the physically relevant solution of Eq (1.4), it is clear that there are special challenges pertaining to identification of the unknown flux function f(u) from observation data. Firstly, it is a challenge with the more indirect characterization of the correct weak solution since it involves formulations like Eq (2.1) and Eq (2.4). This may hamper the use of PINN-based approaches. The approach we take in this work is to rely on a discrete scheme that represents an approximation to the entropy solution described above. A convenient feature of an entropy-consistent numerical scheme is that the entropy condition is automatically built into the scheme. I.e., as the grid is refined, the numerical solution converges to the admissible solution [15,28,29]. Secondly, it follows from the entropy condition Eq (2.4) that observation data that involves one or several discontinuities, may not contain information about the unknown flux function f(u) in intervals that correpond to discontinuities in u. The example shown in Figure 1 shows an approximation to the entropy solution and obeys the entropy condition Eq (2.4). As mentioned above, the example indicates that we lack information about f(u) in the interval ≈[0.3,0.7].
In this work we explore how we can deal with this situation by a proper combination of two different aspects: (i) we add a priori regularity to the unknown flux function f(u) by representing it as a symbolic multi-layer neural network; (ii) we collect observation data by considering a set of different initial data that can help detecting the finer details of f(u).
2.2. Entropy consistent discrete numerical scheme
Based on the given observation data, our aim is to identify a conservation law Eq (1.4) for (x,t)∈[0,L]×[0,T], written in the form Eq (2.5),
where f(u) is the unknown, possible nonlinear flux function and u0(x) is the initial state which is assumed known.
We consider a discretization of the spatial domain [0,L] in terms of {xi}Nxi=1 where xi=(1/2+i)Δx for i=0,…,Nx−1 with Δx=L/Nx. Furthermore, we consider time lines {tn}Ntn=0 such that NtΔt=T. We base our discrete version of Eq (1.4) on the Rusanov scheme [15] which takes the form Eq (2.6),
with j=2,…,Nx−1 and where the Rusanov flux takes the form Eq (2.7),
We use a slightly modified version of the Rusanov flux by relying on a global estimate of |f′(u)| instead of a local estimate of M in terms of Mj+1/2=max{|f′(Unj)|,|f′(Unj+1)|} [15]. The CFL condition [15] determines the magnitude of Δt for a given Δx through the relation Eq (2.8),
We have used ΔtΔxM=CFL≤34<1 when we compute solutions involved in the learning process. The training process involves repeated use of the discrete scheme Eq (2.6) for different flux functions f(u). This requires repeated estimation of the parameters Δt and M that will be used for calculation of predicted data based on Eq (2.6), according to the CFL condition Eq (2.8). Finally, we note that the Rusanov flux falls within the class of monotone schemes and therefore is guaranteed to converge to the entropy solution [28,29,30].
2.3. Observation data set
We consider observation data in terms of x-dependent data at fixed times {t∗i}Nobsi=1 extracted from the solution U(xj,tn)=Unj as follows:
We consider a domain of length L and consider simulations over the time period [0,T]. We apply a numerical grid composed of Nx grid cells when we compute numerical solutions of Eq (2.5) based on the numerical scheme Eq (2.6) and Eq (2.7). This is used both for obtaining the true solution and corresponding synthetic observation data (which we denote by Usub) as well as when we compute predictions based on the ensemble of flux functions brought forth through training (which we denote by ˆUsub). We specify times for collecting the time dependent data
We typically use Nobs=9, with T=1 i.e., Δtobs=0.1. In particular, the number Nobs of collected spatial-dependent data is relatively sparse. Also the number of local time steps (of length Δt) we need to compute numerical solutions through the discrete scheme Eq (2.6) and Eq (2.7) is much higher than the number of observation data, i.e., Δt<<Δtobs. Since Δt is dictated by the CFL condition for the given choice of the flux function f (which will vary during the training), we do not known that ΔtKi=t∗i for i=1,…,Nx for some integer Ki. In that case, we choose the one that is closest to t∗i.
2.4. Main algorithms
Specifically, we use Algorithm 1 to calculate the parameters Δt and M which are needed as input to Algorithm 2. Then, we use Algorithm 2 to extract the solution U(xj,tn)=Unj of the discrete conservation law Eq (2.6). Finally, from {Unj} we extract the observation data set Usub according to Eq (2.9).
2.5. Symbolic Multi-layer Neural Network to represent f(u)
We want to learn the analytical expression of the flux function f(u), not just fit observations using neural networks as a black box. For that purpose we suggest to use the symbolic neural network (called S-Net) proposed in [17] and [18] to learn the unknown function f(u) instead of fully connected neural networks that have been used in, e.g., [11]. We also tested a graph neural network (GNN) method proposed in [31] to learn the hidden conservation law. The GNN method is based on using an evolution scheme of the form Un+1j=Unj+Δt(ΔU)nj where (ΔU)nj must be learned at each grid point. The authors of [31] employed GNN in the context of learning convection-diffusion equations. However, this approach did not work well for the problem Eq (2.5). The reason may be related to the fact that, in our case, the solutions of the hyperbolic conservation law become discontinuous, whereas the PDE models studied in [31] have regular solutions.
In the S-Net setting, depending on whether we seek a function that takes a multiplicative form or a fractional form, we design two types of network structures illustrated, respectively, in Figure 2 (top) and Figure 2 (bottom). Take a three layers S-Net which can learn the expression of a function f possessing a multiplication form as an example. As shown in Figure 2 (top), the identity directly maps u from input layer to the first hidden layer. The linear combination map uses parameters w1 and b1 to choose two elements from u and are denoted by α1 and β1.
These two elements of α1 and β1 are multiplied in the PDE system.
Apart from u gotten by the identity map, f1 also is input to the second hidden layer.
Similarly with the first hidden layer, we get another combination f2(α2,β2).
Then we obtain α3 and β3 by means of w3 and b3 from u, f1 and f2.
f3, which is the product of α3 and β3 is put into the third hidden layer.
Finally, we arrive at the analytic expression of the function f.
The difference between S-Net for multiplicative function (denoted S-Net-M) and S-Net for division function (denoted S-Net-D) is that in the third hidden layer in Figure 2 (bottom), we obtain the numerator part f3 and the denominator part f4 of the flux function f(u) based on w3, b3 and w4, b4, respectively.
The analytic expression of the flux function f is the combination of f3 and f4.
The parameters involved in the network described above is denoted by θ and the resulting function according to Eq (2.17) or Eq (2.20) is denoted by fθ(u). Herein, for the case above the ensemble of parameters used in the multi-layer symbolic neural network is given by
2.6. General architecture
The overall architecture of the method is shown in Figure 3. There are two parts involved, the generation of observed data based on the true flux function f(u) and learning of the unknown flux function fθ(u) which is assigned the S-Net structure. For the synthetic observation data, we use Algorithm 2 to obtain the approximate solution U of Eq (2.5) based on the exact flux function f(u) combined with the scheme Eq (2.6). We select data Usub at times as given by Eq (2.9). Concerning the learning process, firstly, we use S-Net to represent the function fθ(u). fθ(u), together with T,Nx,L,u0 are fed into the DataGenerator to get the predicted solution ˆU. We also choose data ˆUsub at the same time points Eq (2.9). The difference between Usub and ˆUsub is denoted as loss, and we use the second-order quasi-Newton method, L-BFGS-B ([32,33]), to update the parameters θ of the S-Net involved in fθ(u). This updating process iterates until we reach the number of epoch that we set or the process can't be optimized anymore. The learning process is shown in Algorithm 3 which we denote as ConsLaw-Net. Finally, we get the best flux function fθ∗(u) and use it to represent the learned conservation law for further predictions.
2.6.1. Loss Function
We adopt the following loss function for the training of the S-Net function:
where data approximation Ldata is obtained as follows: Assume that we have K different initial states used for the training process, and each predicted solution is described on a grid of N=Nx grid cells and at I=Nobs different times, as given by Eq (2.10). Through Algorithm 3 (ConsLaw-Net) the observation data set is first obtained, which is denoted by {Usub,k(xj,t∗i):1≤k≤K;1≤j≤N;1≤i≤I}. Then, through an iterative loop in Algorithm 3, the predicted data is generated and is denoted by {ˆUsub,k(xj,t∗i):1≤k≤K;1≤j≤N;1≤i≤I}. So we define the data approximation term Ldata as:
3.
Learning of nonlinear flux functions involved in complex fluid displacement
In this section, we consider a class of nonlinear conservation laws that naturally arise from the problem of studying displacement of one fluid by another fluid in a vertical domain. The resulting displacement process involves a balance between buoyancy and viscous forces. Depending on the property of the fluids that are used, there is room for a whole range of different type of displacement processes. This is expressed by the fact that one can derive a family of flux functions which takes the form [34]
The parameter represents the balance between gravity (bouyancy) and viscous forces and, typically, . Different values of result in different types of flux functions. As shown in Figure 4, the shape of varies over a broad spectrum with . In particular, we see that can be purely concave , but also have both one and two inflection points where the sign of changes.
In the following we generate synthetic data by specifying and a class of initial data . We consider a spatial domain such that and consider solutions in the time interval with . We collect observation data in the form Eq (2.9). The aim is to identify the unknown for . Since the solution of Eq (1.4) is TVD (total variation diminishing) [16,29], we know that the solution at any time does not contain any new maxima or minima as compared to the initial data , i.e.,
This feature is inherited by the discrete scheme Eq (2.6) we use [29,30]. In order to learn for , we therfore consider a set of initial data such that . As the solution evolves over time, and corresponding observation data are collected in the form Eq (2.9), we hopefully can extract data which is sufficient to learn a reliable approximation to the true flux function.
As initial data we choose box-like states that give rise to Riemann problems, one at each initial discontinuity. Some of the questions we are interested in are:
(a) How much data do we need for learning the unknown flux function ?
(b) How is the result of the learning of sensitive to noise in the observation data?
(c) How is the question in (a) and (b) sensitive to different flux functions, i.e., to different in light of Eq (3.1)?
(d) What is the role of using S-Net-M versus S-Net-D when we seek to identify the unknown flux function?
In the following we apply a numerical grid composed of grid cells. We test effect of using finer grid in Section 4. We consider observation data Eq (2.9) with
3.1. Example with concave flux corresponding to in Eq (3.1)
We use the S-Net-M given by Eq (2.17) to represent the unknown flux function . We use three hidden layers, and the total number of trainable parameters is then 23. (Note that we obtain the same type of result by choosing S-Net-D since this is a special case of S-Net-M.)
3.1.1. The case with noise-free observations and one initial state
(a) Simulated observation data
We use Algorithm 2 to generate the (synthetic) observations which are sampled at times Eq (3.2) based on the following initial state:
The distribution of observation data is shown in Figure 5 (top) where right plot is a zoomed in version of the left plot. This plot shows that essentially the whole interval is represented in the data suggesting that a good learning of in this interval is possible.
(b) Training and testing
By applying Algorithm 3 (ConsLaw-Net), we obtain after training a flux function which we denote by . The analytical expression of it is given in Table 1. Apparently, differs from the true one. However, we recall that what matters is the derivative . In order to compare with the true flux function, we plot the translated function (revised) in Figure 5 (bottom). Clearly, ConsLaw-Net has the ability to identify the true flux function with good accuracy for the flux . This may not be a surprise since the nonlinearity is somewhat "weak" for this case.
3.1.2. What is the effect of adding noise to observation data?
(a) Simulated noisy observation data
To test the robustness of ConsLaw-Net, we add 5% noise on the data generated by the initial state Eq (3.3) based on sampling times Eq (3.2). That is, we replace by , where and is generated from a uniform distribution. Since varies within we refer to this as noise. The distribution of observations is similar to the one shown in Figure 5 (not shown). Specifically, Figure 6 shows a comparison of noise-free and noisy data at three time points: 0.3, 0.6 and 0.9.
(b) Training and testing
In Figure 7 (top), we show the learned function generated by ConsLaw-Net as well at the translated (revised). Comparison with the true reveals that the noisy data has made the identification slightly less accurate. Figure 7 (bottom) presents a comparison of the solution based on and the predicted solution at later times , by using Algorithm 2 combined with . Noise has been added to the initial data Eq (3.3) and then used with the learned as input to Algorithm 2. This gives rise to the blue dashed line which contains some smaller oscillations due to noisy initial data. From Figure 7 we see that the noisy data combined with just one initial state Eq (3.3) leads to some loss of the predictive ability of ConsLaw-Net. Next, we test how the learning can be improved for the case with noisy data by adding more initial data, thereby, more observation data.
3.1.3. Can we improve the learning when observations are noisy by using 3 initial states?
(a) Simulated noisy observation data
We use Algorithm 2 to generate observations based on the 3 initial states given in Table 2. We have no preferences other than that we want to generate observation data over a broader spectrum by selecting box-functions of different heights as initial states. We consider observation data at times Eq (3.2) and add 5% noise. The distribution of the resulting observation data is shown in Figure 8 (top). Compared to the distribution corresponding to initial data Eq (3.3) and shown in Figure 5, we see that all values of in are to a larger extent represented.
(b) Training and testing
Table 3 shows the analytical expression of the trained obtained by ConsLaw-Net. In Figure 8 (bottom) we see from the plot of (revised) that the increased observation data set resolves the problem with loss of accuracy due to noisy data.
3.2. Example with in Eq (3.1)
We consider now the situation when synthetic data is generated from Eq (3.1) with . From Figure 4 it is clear that the shape is more complex. We use the same S-Net-M as for the previous example to represent , i.e., three hidden layers and 23 trainable parameters.
3.2.1. Noise-free observation data and one initial state
(a) Simulated observation data
We use Algorithm 2 to generate observations based on the following initial state
Observations are extracted at times Eq (3.2). The distribution of observations is shown in Figure 9.
(b) Training and testing
In Figure 10 (top, left), the function obtained from application of ConsLaw-Net and its translated version is shown and compared to the true . Interestingly, we see that is essentially a good approximation of the upper concave envelope of , which is the function involved in the construction of the entropy solution associated with the initial discontinuity of Eq (3.4) located at [15,30]. The initial jump at , on the other hand, relies on the lower convex envelope which amounts to the straight line which connects and and reveals no information about for .
In Figure 10 (top, right), we show that the loss function tends to zero, which reflects that the (wrongly) identified flux function is largely consistent with the observation data. This brings to the surface a main challenge with learning the unknown flux function, namely, the lack of one-to-one correspondence between observation data and nonlinear flux function, as expressed by the entropy condition Eq (2.4). The consequence of this poor approximation to the true is illustrated in Figure 10 (bottom), which presents a comparison of the exact analytical solution and the solution predicted by at times , based on the initial state Eq (3.4). From Figure 9 we see that the observation data is sparse for and for centered around 0.8. So we may try to collect more data from these intervals by adding another type of initidal data.
3.2.2. Can learning of be improved by using 2 initial states?
(a) Simulated observation data
We use Algorithm 2 to generate new observations based on the two initial states given in Table 4.
The distribution of the resulting observation data is shown in Figure 11 (top). Clearly, the part of the interval which was poorly represented with only one initial state, is now present to a larger extent.
(b) Training and testing
The analytical expression of the trained flux function is given in Table 5. From the visualization in Figure 11 (bottom), we see that the learned is largely consistent with the exact with only a small inaccuracy seen in the interval .
Finally, we also want to test the effect of noisy data for this case. We add 5% noise on data generated by the initial state in Table 4. Table 6 shows the analytic expression of obtained by ConsLaw-Net. The corresponding visualization in Figure 12 reflects that the noise hides for the shape of the true flux function, similarly as for the case with less observation data seen in Figure 10.
A natural remedy is to collect more observations by adding a wider spectrum of initial states, as shown in Table 7.
The corresponding histogram showing the distribution of different values of is found in Figure 13 (top). Clearly, the additional initial states has increased the involvement of values in the whole interval , suggesting that a better learning can be expected.
Table 8 shows the analytic expression of obtained from ConsLaw-Net. Figure 13 (bottom) confirms that the learning of the true is quite effective now despite noisy data.
3.3. Example with and defined by Eq (3.1)
We consider the situation when synthetic data is generated from Eq (3.1) with . From Figure 4 it is clear that the shape involves two inflection points. First a convex region for small , followed by a concave for intermediate , and then a convex region again for large . We use the same S-Net-M as for the previous example to represent , i.e., three hidden layers and 23 trainable parameters. Also the times for observation data is given by Eq (3.2).
3.3.1. Noise-free observations and two initial states
(a) Simulated observation data, training and testing
We use Algorithm 2 to generate the observations based on two initial states as specified in Table 9. The corresponding histogram is shown in Figure 14 (top) and suggests a fair chance to achieve good learning result. The result of the learning is illustrated in Figure 14 (bottom). We see that to a large extent the learned fits well with the true with room for improvements in the intervals and .
Now we focus on the case with true flux function . As seen from Figure 4, the shape bears clear similarity to the case with . However, the convex and concave regions are more pronounced. Hence, in light of the result for we may expect that more observation data is required. Therefore, we consider six initial data as given in Table 10.
The distribution of observation data is shown in Figure 15 (top). It reflects a good distribution apart from a somewhat low representation for . The analytical expression of generated by ConsLaw-Net is given in Table 11. The visualization in Figure 15 (bottom) shows that the learned largely captures the variations of the true flux function , with a small loss of accuracy in the interval with sparse observation data ().
3.4. Example with in Eq (3.1)
In this example we explore how ConsLaw-Net can learn the flux function . As seen from Figure 4 this flux function also has two inflection points. The order of the convex and concave regions is interchanged, as compared to the case with , where a convex region for intermediate -values now is surrounded by a concave region for small and large . As before, we use S-Net-M to represent , however, we use four hidden layers which amounts to 34 trainable parameters.
3.4.1. Noise-free observation data and two initial states
(a) Simulated observation data
We use Algorithm 2 to generate the observations based on the two initial states given in Table 12. We generate observation data at times given by Eq (3.2), in addition to the times and . This gives rise to the distribution of observation data as shown in Figure 16 (top). Clearly, the observation data covers the whole interval well.
(b) Training and testing
From Figure 16 (bottom), we see that the learned flux essentially captures the lower convex envelope of the true . In particular, there is a lack of information about the true flux for and . This can be understood in light of the fact that the decreasing initial discontinuity located at and , respectively, depends on the upper concave evelope, which essentially is the straight line which connects and . Hence, precise information about the shape of is difficult to reveal. As a result, the initial increasing jumps at and , respectively, then imply that ConsLaw-Net generates a function which coincides with the lower convex envelope of , as shown in Figure 16 (bottom).
3.4.2. Improving the learning of by using six initial states
(a) Simulated observation data
We increase the number of initial data from two to six, as shown in Table 13. We use Algorithm 2 to generate the observations based on initial data in Table 13. The corresponding histogram of observation data is shown in Figure 17 (top).
(b) Training and testing
We first illustrate in Table 14 the analytical expression of the learned flux function obtained through ConsLaw-Net. From Figure 17 (bottom) we see that is consistent with the exact with respect to in most intervals, except for the interval . Combined with the observation distribution in Figure 17 (top), we see that there are relatively few observations in this interval, which most likely is the reason for this loss in accurate learning.
4.
Learning of fractional flux functions
In this section, we consider a flux function in the following fractional form Eq (4.1)
This nonlinear flux function appears in the context of creeping two-phase porous media flow [15] and accounts for a large range of nonlinear two-phase behavior. We consider the same spatial domain as before () and explore solution behavior in the time period with . We set in Eq (4.1) when we generate synthetic data for further testing of ConsLaw-Net for this class of flux functions. We use a grid of cells and consider observation data Eq (2.9) at times Eq (3.2).
4.1. Example with in Eq (4.1)
We first try to use S-Net-M with three hidden layers and 23 trainable parameters, based on previous experience from Section 3. However, we find that the loss function does not converge to zero, see Figure 18 (left). Therefore, we replace it by S-Net-D (2.20) with two hidden layers and 18 trainable parameters which gives significantly better behavior in terms of convergence behavior of the loss function, see Figure 18 (right).
4.1.1. What is the effect of noisy observations?
(a) Simulation of observation data, training, and testing
We use Algorithm 2 to generate the observations based on initial state in Table 15. Then, 3% noise is added to the observations. The distribution of the resulting observation data is shown in Figure 19 (top). Specifically, Figure 20 shows clean and noisy data corresponding to the first initial data in Table 15 at three time points: 0.3, 0.6 and 0.9.
Table 16 shows the analytic expression of the identified . In Figure 19 (bottom), we see a comparison of the learned flux function under noisy data and the true flux function. Clearly, the learning has been effective for this flux function under noisy data based on ConsLaw-Net combined with the neural network S-Net-D to represent the unknown flux function.
5.
Conclusion
Compared with advanced methods that have been used to learn PDE problems from data [11,13,14], our method can deal with scalar conservation laws and identification of the unknown nonlinear flux function. In this paper, we designed a framework denoted ConsLaw-Net that combines a deep feed-forward network and an entropy satisfying discrete scheme to learn the unknown flux function. We have found that by including observation data from a sufficient number of initial states, the correct nonlinear flux function can be recovered. This is true both for data with and without noise. Using symbolic multilayer neural networks (S-Net-M or S-Net-D) to represent the unknown flux function in an entropy satsifying scheme, represents the key components. It has been demonstrated that the additional regularity imposed on the flux function through helps to identify the correct form of it. Moreover, the identified flux function has the ability to discover the unknown nonlinear conservation law model from a relatively sparse amount of observation data, e.g., typically sampled at 10 different times. Interesting findings are:
Depending on the complexity of the hidden flux function we seek to identify, i.e., the non-linear shape, we may need observation data corresponding to a set of different initial states . This is necessary in order to collect information that can reflect the nonlinear form of for all values of in the interval for which we seek to learn the flux function. We also explore the impact of noise in the observation data and find that the correct flux function to a large extent can be identified from noisy data by including 4–6 different initial states.
We find that the method can learn the relevant flux function for a whole family of different flux functions ranging from pure convex/concave to strongly non-convex functions. The role of observation data as a result of different sets of initial states, is highlighted.
In this work we apply a variant of the Rusanov scheme [15] which relies on an estimate of the maximum value of . The simplicity of the numerical scheme is exploited in the learning process. Other numerical schemes may require suitable modifications in the definition of ConsLaw-Net.
The current version of ConsLaw-Net is restricted to a scalar conservation law in one dimension. Possible further extensions can be: (i) What is the role of the specific discrete scheme that approximates the entropy solution? Does the method work for any entropy-satisfying scheme? (ii) Is it possible to also learn the role played by parameters like in Eq (3.1) and Eq (4.1) from the observation data? In orther words, identify the functional form of with respect to both and . (iii) Explore the proposed method in a setting where experimental data is available. This may lead to considering other type of observation data than we have used in this work.
Acknowledgments
The authors acknowledge the University of Stavanger to support this research with funds coming from the project "Computations of PDEs systems and use of machine learning techniques" (IN-12570).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:





















