1.
Introduction
We consider the system of difference equations
where ε∈[0,1] is a coupling parameter and fμ(x)=μx(1−x), μ∈(0,4], x∈[0,1], is the classical logistic family widely studied [7,25,26]. This model was proposed and studied in [17,18] and it is motivated by difference equations associated to the Belousov-Zhabotinsky chemical reaction [11,12,20,21]. This model is included in the family of the so-called dynamics of coupled map lattices (see e.g. [13,10,5]).
This model can be seen as a convex deformation between two well-known systems. When ε=0, the systems reads as
and so is the product map fμ×fμ, while if ε=1, we have the model
called antitriangular [4]. This kind of map appears naturally in some economic models called duopolies [19,14]. In both cases, the dynamics of this model is deeply connected with that of fμ. In particular, attractors or limit sets of the orbits have been analyzed [1], [4], [19]. From these papers, one can see that a rectangle contained in [0,1]2 can be an attractor or a limit set of these models and suggest a response to the question raised in [17] about the synchronization of the model Eq (1.1). In general, some orbits do not synchronize. We will check this by proving the existence and asymptotic stability of fixed points out of the diagonal Δ={(x,x):x∈[0,1]} in Section 2 and by studying the local stability of the diagonal utilizing Lyapunov exponents in Section 3. The paper finishes with a section in which we study the bifurcation scenarios of the model Eq (1.1) to illustrate and complete the results of the two previous sections.
Of course, a lot of work is left to understand these systems' dynamics. For instance, a complete characterization of the attractors, the existence of chaotic dynamics when simple maps fμ are considered, and how is the chaotic dynamics outside the diagonal Δ. In some sense, this paper is a partial advance for these and other possible questions.
We organize this paper divided into the three sections mentioned above. Each section contains the basic definitions necessary to understand the presented results.
2.
Periodic points: existence and stability
Given a map f:X→X, X⊂Rn, n∈N, we denote by f0 the identity on X, by f1=f, and define inductively fn=f∘fn−1. The solution of the difference equation
is called the orbit of x0 by f. The set of the limit points of the orbit of x0 is called the attractor or the ω-limit set of x0 by f, denoted by ω(x0,f). We say x∈X is periodic of period n∈N if fn(x)=x and fi(x)≠x for 1≤i<n. If n=1 we say that x is a fixed point of f. According to [8], a fixed point x0 is said to be:
1. Locally stable if for each ε>0 there exists a neighborhood V of x0 such that for any x∈V, then ||fn(x)−x0||<ε, for each n∈N.
2. Attracting if there exists a neighborhood V of x0 such that limn→+∞fn(x)=x0 for each x∈V.
3. Locally asymptotically stable (LAS) if it is both, locally stable and attracting.
4. Furthermore, if a fixed point x0 is LAS, then |Jf(x0)|≤1 whenever f is differentiable and Jf(x0) denotes the Jacobian matrix.
Now, fix fμ(x)=μx(1−x), μ∈(0,4], x∈[0,1]. For ε∈[0,1], we define
defined on [0,1]2. The diagonal set
is invariant by Fε,μ, i.e., Fε,μ(Δ)⊆Δ and the dynamics on this invariant set is independent on ε and given by fμ since
In addition, the map Fε,μ is symmetric with respect to Δ, that is, Fε,μ(x,y)=Fε,μ(1−x,1−y) for all x,y∈[0,1].
The equation
gives us the fixed points of Fε,μ. It is easy to see that this equation has at most four solutions Pi, i=1,2,3,4, given by
● P1=(0,0).
● P2=(μ−1μ,μ−1μ).
● P3=(1+(2ε−1)μ−√(1+2ε(μ−2)−μ)(1+(2ε−1)μ)2(2ε−1)μ,1+(2ε−1)μ+√(1+2ε(μ−2)−μ)(1+(2ε−1)μ)2(2ε−1)μ).
● P4=(1+(2ε−1)μ+√(1+2ε(μ−2)−μ)(1+(2ε−1)μ)2(2ε−1)μ,1+(2ε−1)μ−√(1+2ε(μ−2)−μ)(1+(2ε−1)μ)2(2ε−1)μ).
Clearly, P1 and P2 belong to Δ and P2 exists and it is different from P1 if and only if μ≤1. P3 and P4 are symmetric with respect to Δ and do exist whenever
Note that the equation
has solutions
and
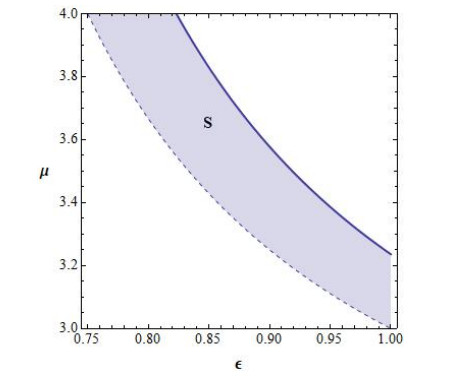
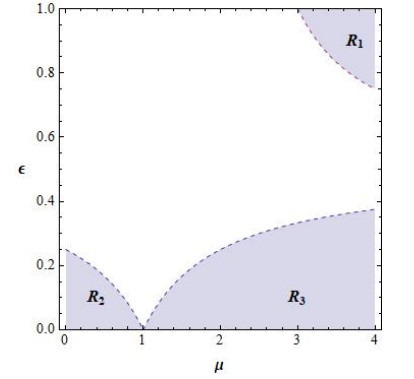
If the conditions Eq (2.1) and Eq (2.2) are fulfilled, then P3=P4=P2. The region where both P3 and P4 exist and are different from P2 can be seen in Figure 1.
However, as
in the regions R2 and R3, the points P3 and P4 have negative coordinates except when ε=0 and μ>3, where the fixed points are P3=(0,μ−1μ) and P4=(μ−1μ,0). Therefore, the region where fixed points P3 and P4 exist and are different from P2 is
where
The Jacobian matrix is
We use it to study the local asymptotic stability of the fixed points of Fε,μ.
2.1. The fixed point P1
The Jacobian matrix reads as
with eigenvalues μ and μ(1−2ε). As |1−2ε|≤1, it turns out that if μ<1, then P1 is LAS.
2.2. The fixed point P2
The Jacobian matrix reads as
with eigenvalues 2−μ and (2−μ)(1−2ε). As |1−2ε|≤1, it turns out that if 1<μ<3, then P2 is LAS.
2.3. The fixed points P3 and P4
By symmetry, the analysis for P4 is the same than that of P3. So, we will study the stability for P3. The Jacobian matrix reads as
with eigenvalues
and
These eigenvalues are real when
The equation
gives the solutions
and
It can be seen that μ1<0 while the graph of min{4,μ2} can be seen in Figure 2, jointly with the region S such that λ1 and λ2 are real.
In this case, note that λ1≥λ2 and the equality holds when λ1=λ2=1−ε1−2ε. The equations
and
are the boundaries of the region with real eigenvalues with modulus smaller than one. The solutions of the equation Eq (2.3) are the ones of the conditions Eq (2.1) and Eq (2.2), while the solutions of the Eq (2.4) are
The first solution satisfies that μ<0. Hence, when the eigenvalues are real, the stability region is given by the inequality
When the eigenvalues are complex, the border of the stability region is given by the equation
which reduces to
with solutions
The first solution satisfies that μ<0. Hence, when the eigenvalues are complex, the stability region is given by the inequality
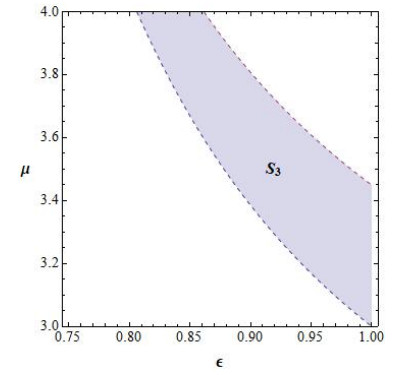
Hence, the stability region of P3 is the set
This region can be see in Figure 3.
Then, we can summarize the above results as follows.
Theorem 1. Let P1, P2, P3 and P4 be the fixed points of the map Fε,μ. Then:
(a) The fixed point P1 is LAS if μ<1.
(b) The fixed point P2 is LAS if 1<μ<3.
(c) The fixed points P3 and P4 are LAS if either ε>0 and (ε,μ)∈S3.
Proof. The cases (a), (b) and case (c) when ε>0 have been studied above. When ε=0, note that P3 and P4 cannot be LAS since the stability conditions of the map fμ to have 0 and μ−1μ cannot be fulfilled simultaneously.
3.
Synchronization
We say that an orbit of Fε,μ synchronizes if its attractor is contained in the diagonal line Δ. The orbit converges therefore to an attractor of the map (1−ε)fμ+εfμ. Here one can identify the diagonal Δ with the interval [0,1]. The attractors of this kind of maps are well-known (cf. [9].). They are of the following types:
1. a periodic orbit;
2. a finite union of pairwise disjoint subintervals I1,I2,…,Ik such that fk(Ii)=Ii and fk|Ii has a dense orbit for i∈{1,…,k};
3. a Cantor set,
and there is at most one metric attractor of a type different from type (1).
Following [3,§2.1], see also [24], for a given v=∑2i=1aivi−1=(a1,a2)β∈R2 (here, we use the subindex β to indicate that its coordinates are expressed in terms of the basis β={(1,1),(1−,1)}), we define the tangential Lyapunov exponent at ˉx in the direction of v to be
where ΠΔ is meant the projection of a vector of R2 in the subspace Δ and dFnˉx denotes the differential of F at ˉx=(x,y). On the other hand, again following [3,§2.1], we define the normal Lyapunov exponent at ˉx∈Δ in the direction of v to be
The existence of fixed points P3 and P4 proves that the dynamics of Fε,μ when μ>μ0=3.5699... need not converge to the diagonal Δ. This fact solves a question stated in [17]. In this section, we will explore when the synchronization of Fε,μ is possible. For that, note that the Jacobian matrix at Δ, given by
is circulant (see [6]). Then,
and
Note that (1,1) is a basis of Δ and (1,−1) is normal to Δ.
Following the ideas from [5], we can prove that
and
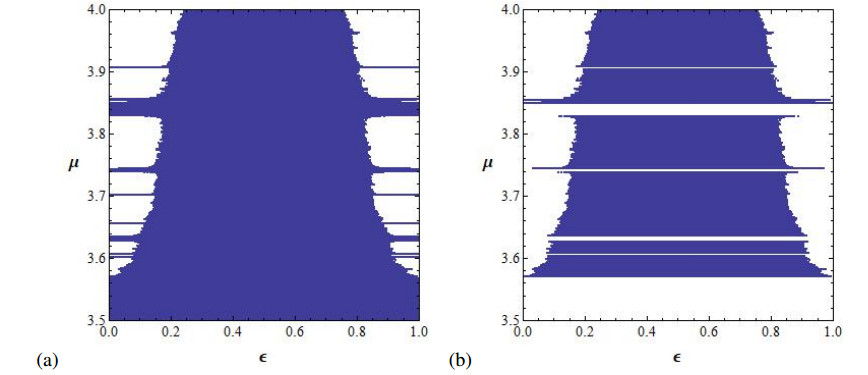
It is known, see [2], [3,Theorem 2.8 and Proposition 2.21], that LE∥(x) measures the complexity along the trajectory of x and LE⊥(x) measures the convergence to Δ, i.e. the synchronization, which is possible when LE⊥(x)<0. A chaotic synchronization is possible when LE∥(x)>0. In Figure 4, we will show the values in the parameter space (ε,μ) where the synchronization is possible.
Note that when ε=0, the map F0,μ is the product map fμ×fμ. When ε=1 we have that F0,μ(x,y)=(fμ(y),fμ(x)), and it is known as antitriangular map. The attractors of product and antitriangular maps have been studied in several papers (see, e.g. [1]).
It is clear that if fμ has two fixed points (μ>1) and ε=0, then there exist orbits of F0,μ that do not synchronize: the fixed points P3=(0,μ−1μ) and P4=(μ−1μ,0). When μ∈(1,3], the fixed point P2=(μ−1μ,μ−1μ) attracts the orbits of all the points with a positive initial conditions while P3 and P4 attract the orbits with initial with one coordinate equal to zero. It is clear that the orbits which do not synchronize increase when μ>3.
4.
Attractors and bifurcation scenarios
Below we show the behaviour of the attractors when ε ranges the interval [0,1]. We see the typical attractor of the product map when ε=0; this attractor is perturbed until the parameter ε enters a region of synchronization, and synchronized attractors contained in Δ are shown. After that, the parameter enters the region S3, where the fixed point P3 is LAS, leaving the stability region via a Neimark-Sacker bifurcation given by complex eigenvalues with modulus one [15]. After that, the circle is perturbed and the attractors evolve to finish when ε=1 of a well-known attractor of an antitriangular map. Figure 5 shows bifurcation diagrams on the variable x for fixed values of μ and ε ranging the interval [0,1].
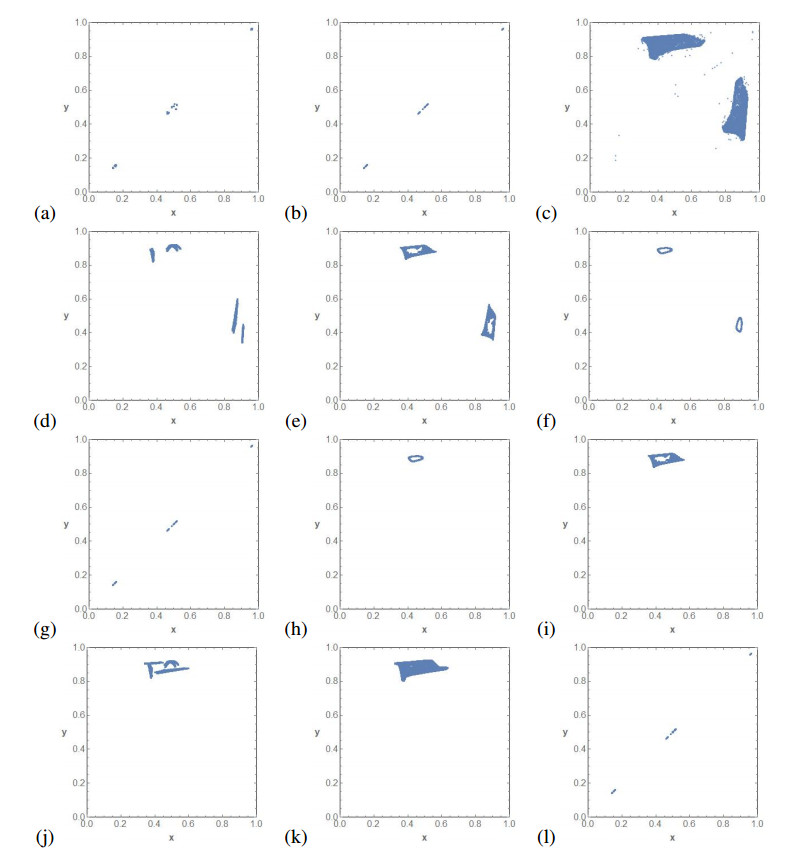
The information of Figure 5 is not complete. Only the variable x is shown, and some additional information is necessary to have a complete picture of know the shape of the attractors. So, we add figures of different orbits with both coordinates and explain how the bifurcations behave. It is important to realize that Figure 5 is shown the projection to the X-axis of attractors of the plane and that different shapes can give rise to the same projection. For instance, the projections on the X-axis of a closed curve and a rectangle can be the same interval, although the dynamics can be completely different. So, Figures 6–9 are useful for a better understanding of Figure 5.
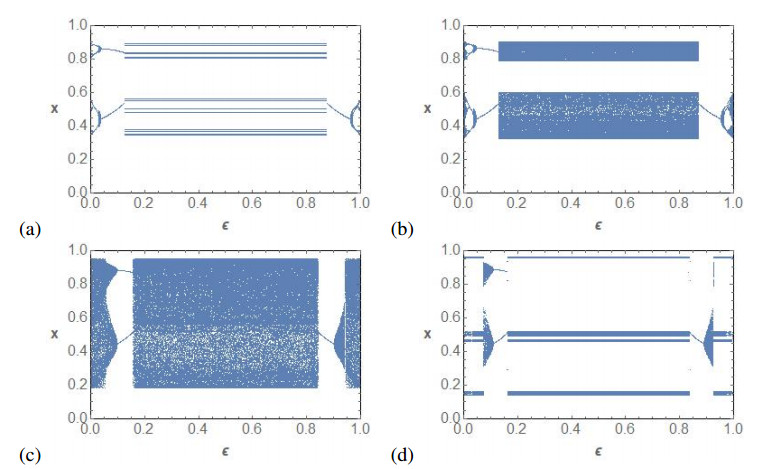
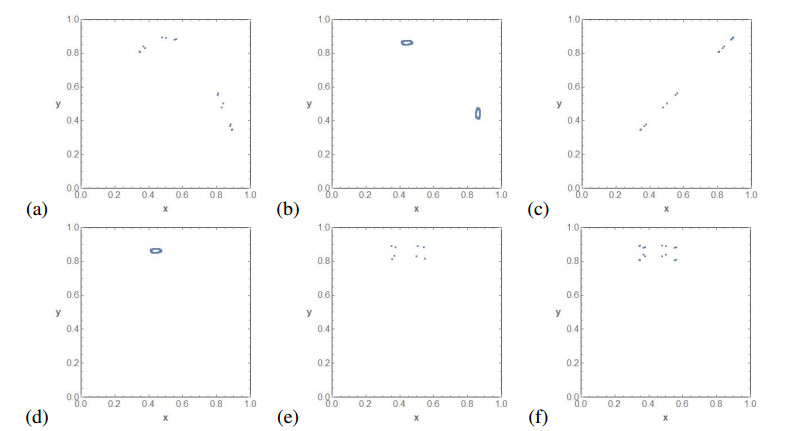
Figure 6 completes the bifurcation diagram of Figure 5a. We show six phase space plots for several values of ε when μ=3.568. Note that for μ=3.568, the map fμ is not chaotic and almost all the orbits all attracted by a periodic orbit. So, in (a) we can see a periodic attractor of F0,μ, which evolves periodically until we meet a Neimark-Sacker bifurcation in which a two periodic orbit bifurcates into two periodic curves. The curves collapse to a two periodic orbit until we reach the synchronization. When ε is big enough, so no synchronization is possible, we have fixed points which evolve to an invariant curve via a Neimark-Sacker bifurcation. When the invariant curve disappears, we have periodic orbits again.
Figure 7 completes the bifurcation diagram of Figure 5b. First, we have a non-synchronized orbit of F0,μ shown in Figure 7a, which evolves until we enter the parameter region where synchronization is possible. In Figure 7b, we show an intermediate attractor. This region of synchronization is reached by a periodic orbit of period two. The attractor in Δ is shown in Figure 7c. The region where synchronization is possible breaks to a fixed point, and after a Neimark-Sacker bifurcation Figure 7d, and then the attractors evolve to get a typical attractor with a non-empty interior of the antitriangular map F1,μ in Figure 7f. Figure 7e shows an intermediate step between the synchronization region and the antitriangular map.
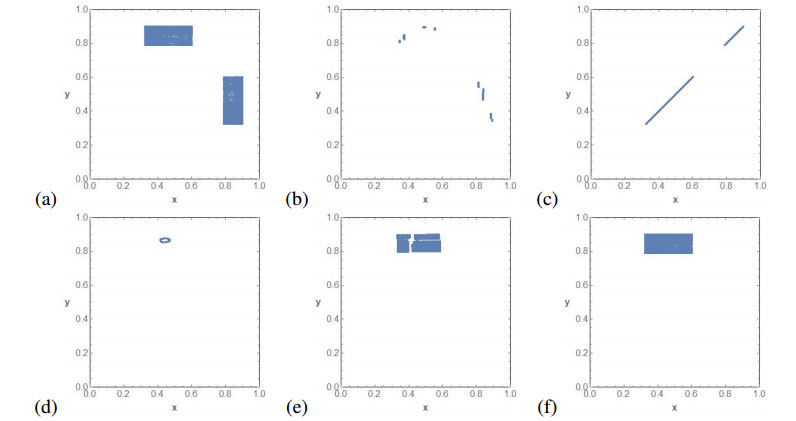
Figure 8 completes the bifurcation diagram of Figure 5c. We start by showing the attractor of F0,μ, which evolves following Figures 8b–d and degenerates to a periodic orbit via a Neimark-Sacker bifurcation Figure 8e. When the parameter ε enters the region where synchronization is possible, we have Figure 8f. Then, the system synchronizes Figures 8g and leaves the synchronization region Figure 8h, followed by a fixed orbit which bifurcates to a closed curve via a Neimark-Sacker bifurcation. The curve degenerates to several attractors, Figure 8j and Figure 8k until we arrive at the final attractor of the antitriangular map Figure 8l. It is worth pointing out Figures 8f, h. They indicate that when the parameter ε is going to enter the synchronization region, a two periodic orbit "explodes" to an attractor with unclear structure. The same happens when ε leaves the parameter region where the orbits of x and y synchronize in Δ.
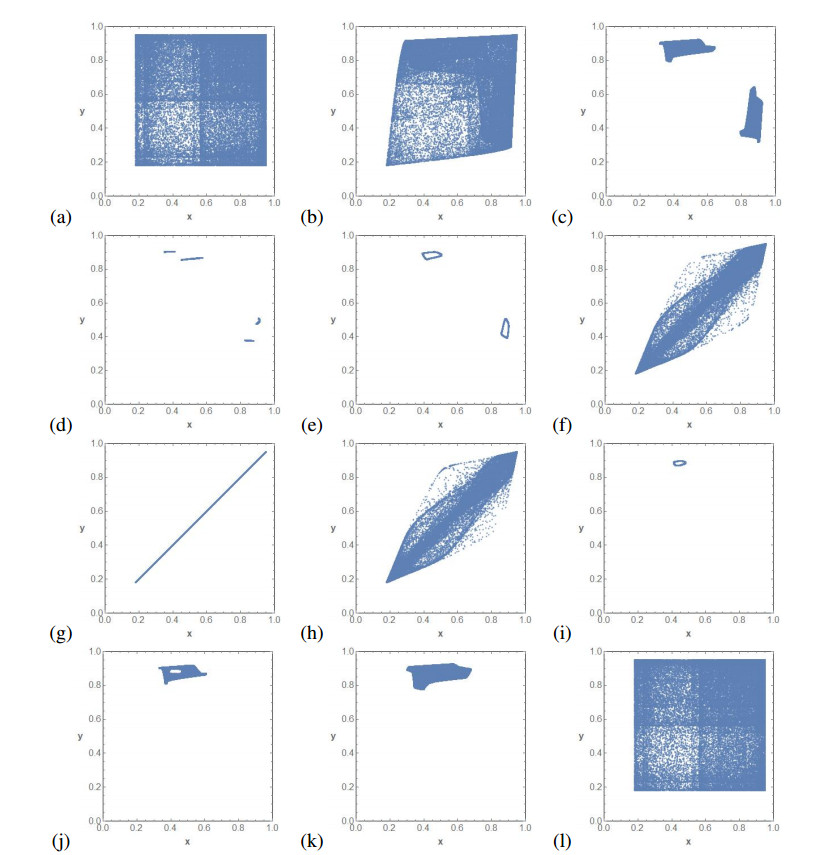
Figure 9 completes the bifurcation diagram of Figure 5d. Figure 9a shows the attractor of F0,μ. Then, Figures 9b–f show the route to synchronization parameters Figure 9g. Note that we arrive at this parameter region after a Neimark-Sacker bifurcation of a periodic point of period two. After the synchronization, we have a fixed point which bifurcates to a periodic curve Figure 9h, which degenerates Figures 9i–k. Finally, we get the attractor of the antitriangular map Figure 9l.
Remark 1. As stated in [17], since Δ is invariant by Fε,μ and the dynamics restricted to Δ is given by the dynamics of fμ, we know that some complex behavior can found when μ>μ0=3.5699... as the topological entropy of fμ is positive (see [5] for further discussions on this issue). When μ<μ0 the topological entropy of fμ is zero and the Lyapunov exponents are negative, and the unique possible attractors are periodic orbits. Thus the diagonal Δ is free of complexity, but it is unclear whether it is possible to have a complicated behavior when the dynamics are outside Δ. Figure 6 shows the existence of an invariant closed curve. Still, it is unclear whether the dynamics on this curve are complicated or not since it could be conjugate to an irrational rotation. Additionally, we did not observe the existence of attractors that can have positive two-dimensional Lebesgue measure.
5.
Discussion
Although this paper considers the logistic map, we present a general method to decide whether a coupled two-dimensional system can locally synchronize to the diagonal. This result completes the paper [5], where the method was presented for dimensions greater than two. The process to estimate Lyapunov exponents depends on the fact that the Jacobian matrix on the diagonal is circulant and can be easily adapted for different types of coupling, for instance, linear coupling. The bifurcation diagrams, jointly with the shown orbits, illustrate the results. This author would be surprised if significant new phenomena are shown when the logistic map is replaced with another regular enough one-dimensional map. It is substantial to find conditions to guarantee that almost all orbits in the system converge to the diagonal. Still, this question is challenging to solve because the dynamics of two-dimensional systems are far from being characterized.
6.
Conclusion
We have considered a two-dimensional coupled map based on the one-dimensional logistic family. We can see this system as a deformation through the coupling parameter ε with a product map from one side and an antitriangular map from the other. Then, we use the fact that the Jacobian matrix at the diagonal is circular to give an explicit formula to estimate Lyapunov exponents and analyze when the system can locally evolve to synchronize their orbits in both chaotic and non-chaotic ways. We have obtained evidence that the dynamics when ε is close to zero are a distortion of the dynamics when ε=0. A similar result is obtained for ε=1. So, the dynamics evolve from the case ε=0 to ε=1 through a huge parameter region where orbits synchronize. We must emphasize that the method described in this paper can be easily adapted for systems based on regular enough one-dimensional maps different from the logistic family considered in this paper.
Acknowledgements
I thank the two anonymous referees for their comments and suggestions to improve this manuscript.
This work has been supported by the grant MTM2017-84079-P funded by MCIN/AEI/10.13039/501100011033 and by "ERDF A way of making Europe", by the "European Union".









 DownLoad:
DownLoad: