1.
Introduction
For the actual neural network system, it will be affected by the outside world or its own system, which will lead to the deterioration of the stability and even the instability of the system. Therefore, when the neural networks with fractional-order (FO) derivative are selected as the research target, it is necessary to consider the above effects. And then, it is an important topic to analyze the stability of the system and how to design a system synchronous controller simply and effectively. Only by doing these things well can we effectively use the FO neural network and apply it better in practice. Synchronization is one of the dynamic behaviors of actual systems, which exists widely in real life. Therefore, studying the synchronization of FO neural network models is meaningful and extremely important. In view of this, a lot of scholars have paid attention to the synchronization issues of neural networks with FO derivative, see [1,2,3,4,5,6,7] and the references therein.
Yu et al. [8] analyzed the following neural networks with FO derivative in 2014
where 0<α<1. Based on some analytical techniques and combining effective control method, some new criteria for guaranteeing the projection synchronization of the neural networks with FO derivative are achieved. In 2015, Bao et al. [9] investigated the projective synchronization of FO memristor-based neural networks corresponding to model (1.1) and achieved some sufficient conditions by utilizing a FO differential inequality. In 2018, Hu et al. [10] studied the neural network model (1.1), and the global synchronization problem was considered. Firstly, some properties for fractional calculus are discussed, and the stability theorem for the neural network model (1.1) is proposed. Moreover, a new feedback controller is given. Finally, some sufficient conditions ensuring the global synchronization of the neural network model (1.1) are given by utilizing the matrix inequality technique and the obtained stability theorem. However, it can be seen that there is no delay term in model (1.1). Because time delays are inevitable in practical network fields, the real-world neural network model should contain time delays. Therefore, in recent years, more and more scholars focus on the dynamic behavior of delayed neural networks with FO derivative. For example, Wang et al. [11] researched the following delayed FO Hopfield neural network as described below in 2015
where q∈(0,1),ai,bij,cij are constants, and acquired some stability conditions of solution for the FO network system (1.2) according to the Laplace transform and linearization method. In 2017, Peng et al. [12] considered the following FO neural networks with time delays and discontinuous activation functions
where x(t)=(x1(t),x2(t),⋯,xn(t))∈Rn is the state vector of neuron at time t. Several sufficient conditions ensuring the global synchronization of neural networks (1.3) are given by using the property of matrix inequalities and the theory of FO differential inclusion. Zhang et al. [13] paid attention to the following neural networks with FO derivative and delays in 2018
where 0<α<1,iϵN=1,2,…,n, and derived several new synchronization conditions of the delayed system (1.4) by utilizing the corresponding theoretical knowledge. In 2020, Wang et al. [14] investigates the problem of event-based sliding-mode synchronization of memristive neural networks with delay by means of continuous/ periodic sampling algorithm. More recently, in 2021, Wang et al. [15] considered the multiple delayed FO neural networks with Caputo derivatives as described below
where 0<α<1, and obtained some synchronization conditions of the delayed FO neural networks (1.5) by constructing a suitable Lyapunov function and using the properties of delayed differential inequality. In 2022, Hui et al. [16] investigated a kind of variable-delay FO complex-valued neural networks and achieved the adaptive synchronization results of the network system, Ye et al. [17] considered a kind of variable-parameter FO neural networks and obtained two types of quasi-synchronization results of the network system, and Zhao et al. [18,19] discussed respectively PID control, adaptive control, pinning control, and impulsive control for a class of complex networks.
On the other hand, as we all know, it is challenging to obtain the exact values of model parameters when we build mathematical models. The main reason is the environmental disturbance that leads to parameter uncertainty. Hence, when we discuss the dynamic properties of nonlinear systems, we cannot ignore the effect of these parameter nondeterminacy, because parameter indeterminacy will damage the synchronization, stability, or any other performances of the nonlinear system. Recently, the synchronization of neural network models with parameter nondeterminacy has received extensive attention from many scholars, such as Yang et al. [20] in 2018 considered the parameter nondeterminacy to study a kind of FO memristor-based complex-valued neural networks described below
and several effective global asymptotically synchronization results of the neural networks system (1.6) are obtained. It is particularly worth mentioning that Wang et al. [21] researched the nonautonomous delayed neural networks with FO derivatives as described below in 2020
Firstly, the authors obtained the analytical formula of the synchronous controller for the delayed neural networks (1.7) according to the new state control schemes and Mittag-Leffler function. Secondly, by improving some new analytical techniques, using delay differential inequalities and building appropriate Lyapunov functions, the authors achieved several sufficient conditions to ensure the global synchronization of the FO nonautonomous delayed neural networks (1.7).
However, in the existing work, nonautonomous delayed FO neural networks (DFNNs) have rarely been discussed. Because of the fact that the self-inhibition rate and the connection weight between neurons in the neural networks should be a time-varying function, not a constant, the nonautonomous DFNNs can preferably simulate the interaction between neurons in the network system. Therefore, inspired by the existing work, the purpose of this article is to research the synchronization of a nonautonomous DFNNs with Caputo derivatives. By constructing the Lyapunov function, the asymptotic stability of zero solution for the error system is verified, and some sufficient conditions are achieved to ensure the global synchronization behaves well. The remainder of this work is organized as follows. In Section 2, some definitions and lemmas are presented, and new neural networks are proposed. In Section 3, the global asymptotically synchronization controller is obtained, and some criteria ensuring the global asymptotically synchronization for the new neural networks are afforded. In Section 4, the feasibility of the obtained theoretical results is shown by some numerical simulations. In the last part, the conclusions are summarized.
Remark 1: As we all know, there is no general rule in the design of the synchronization controller of the neural network, which brings difficulties and challenges to the design of the controller. An excellent controller should have two main characteristics: first, it is simple and easy to realize, and second, it has good robustness. The following is the summary of contributions and innovations of this article: (1) In order to preferably represent the interaction between neurons, new neural networks are proposed by introducing the variable-parameters into the known DFNNs. Our new model cover the autonomous DFNNs and FNNs with Caputo derivatives in the literature. (2) Utilizing the delayed FO differential inequalities and Razumikhin-type stability theorem of the delayed FO differential system, some sufficient conditions are achieved to ensure the global synchronization of studied neural networks. In particular, our synchronization control scheme has strong robustness to the above new model. (3) In contrast with the previous works in the literature [8,12,13,21], our controller is simpler and easier to implement. Secondly, our criterion for ensuring the synchronization of drive-response systems is easier to verify, which can provide more convenience for the application by using these results into DFNNs.
2.
Problem statement
In this article, R is a real space, and Rm is an m-dimensional Euclidean space. The norm ‖⋅‖ in Rm is expressed as an arbitrary norm and N+ is a set of positive integers. Next, we will recommend several definitions and lemmas.
Definition 1. [22,23] The fractional integral of the integrable function x(t) is defined as
where t⩾t0, order α>0. Γ(⋅) is a Gamma function, which is defined as
It is obvious that Γ(α) satisfies recursive relationship Γ(α+1)=α Γ(α).
As above mentioned, the Caputo FO derivative has a more practical significance in the physical system and is more suitable for describing the actual system with the initial value than the Riemann-Liouville (R-L) FO derivative and the Grunwald-Letnikov (G-L) FO derivative. Thus in practical applications, the Caputo differential operation is more used than the R-L differential operation and the G-L differential operation. So, the definition of the Caputo FO derivative will also be used in this paper.
Definition 2. [22,23] The Caputo FO derivative of function x(t)∈Cn([0,∞),R) is defined as
where α represents the order of the derivative.
In particular, when 0<α<1, there is
Lemma 1. [22] For any constant c1,c2, if w(t),u(t)∈C([t0,+∞),R), α>0,β>0, then
Lemma 2. [24] Set f(t)∈Rn is a differentiable vector value function, P∈Rm×n is a symmetric positive definite real matrix, then we have the following inequalities
where α∈[0,1], s⩾s0.
Lemma 3. [25] If there is a continuously differentiable function V:R×Rn→R and two positive constants p,q with p<q such that
for , then the differential system with Captuto derivative
is globally asymptotically stable.
In this article, a non-autonomous DFNNs with Caputo derivative are researched, and the systems are described as follows
or written as a vector form
where represents the number of neurons, represents a state variable of neuron at time , represents the propagation delay of the neuron, represents a state variable of neuron at time , and denote an excitation function of a neuron, denotes a self-joining weight matrix of a neuron, denotes an internal connection weight matrix when there is no time delay, denotes an internal connection weight matrix when there exists time delay, and denotes an external input vector.
3.
Synchronization of nonautonomous DFNNs
In this section, the synchronization of the nonautonomous DFNNs with Caputo derivative are studied and several sufficient results are given. In this work, if we regard the system (2.8) as the driving system, the following is the corresponding response system
write as a vector representation
here represents a state variable from the system (18), the representation of is consistent with the drive system (2.8), represents the synchronous controller of the system.
Set the error vector , then the expression of the error system can be obtained from the drive system (2.8) and response system (3.1)
write as a vector representation
where
Through analysis, it can be found that the global synchronization of drive-response system (2.8) and (3.1) is equivalent to the global asymptotic stability of the zero solution for error system (3.3). In this article, the activation function is a common Lipschitz continuous, and the following assumptions are necessary to prove the main conclusions of this paper.
Suppose that there exist constants , such that
for all
Suppose that , and each element in matrices is bounded function.
Theorem 1. Assume that assumption and are satisfied, then the driving systems (2.8) and response system (3.1) are globally asymptotically synchronized under the controller as follow
where depends on
Proof: Let
here and which satisfies can be appropriately selected.
Constructing the Lyapunov function
From the assumption , it holds that
According to the assumption Lemma 1, Lemma 2, the Eqs (3.3), (3.5) and (3.9), the Caputo derivative of along the system (3.3) is as follow
According to the trigonometric inequality, we can get
thus, from Eqs (3.10) and (3.11), it holds that
Moreover, for any given , there exists a such that
From Eqs (3.12) and (3.13), we have
Base on Lemma 3 and Eq (3.14), under the controller Eq (3.5) the zero solution of the error system (3.3) is globally asymptotically stable. That is to say, the drive system (2.8) and the response system (3.1) is globally asymptotically synchronized. This complete the proof of Theorem 1.
4.
Numerical experiment
In this section, the effectiveness of results for FO delayed nonautonomous neural networks Eq (2.8) is shown by a numerical example. The numerical simulation of the instantiated system is carried out by MATLAB simulation software, and the simulation results are analyzed to verify the correctness of the above theoretical analysis and derivation.
Example 1. Consider the two-dimensional non-autonomous DFNNs with Caputo derivative Eq (2.8). Matrices of the self-joining weights and of the internal connection weights at present as well as of the internal connection weights at the delay time for the neural networks Eq (2.8) are selected as
Set the state variable at time the delay the derivative order the external input vector and the activation function vectors Thus, the numerical simulation model of the drive system is as follows
note that assumptions and are satisfied with . Set the controller return matrix , thus, the state-feedback controller is designed as follows
Therefore, the numerical simulation model of the response system is as follows
Through simple calculation, we can get So the conditions of Theorem 1 is satisfied. According to Theorem 1, the drive-response systems (4.1) and (4.3) from the nonauto- nomous DFNNs with Caputo derivative are globally asymptotically synchronized.
The initial values of the drive system (4.1) and the response system (4.3) are taken as follows
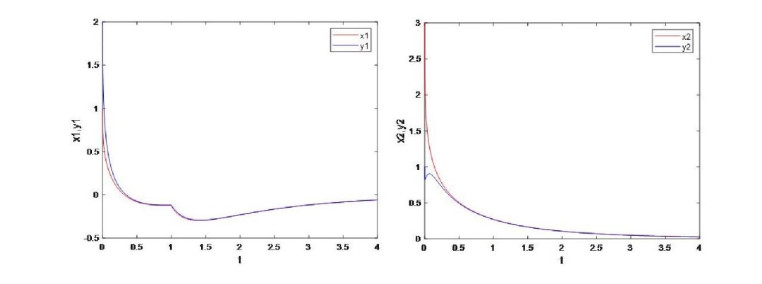
The solutions of the drive-response systems (4.1) and (4.3) with the initial values Eq (4.4) are shown in Figure 1. Moreover, the differences between the components of both solutions are shown in Figure 2. As it can be shown, these differences approach 0 very fast. From Figures 1 and 2, it is easy to determine that the drive-response systems (4.1) and (4.3) with the initial values Eq (4.4) are globally asymptotically synchronized. And then, the conclusion of Theorem 1 is verified.
To further verify that the drive-response systems (4.1) and (4.3) are globally asymptotically synchronized, different initial conditions, different fractional orders, and different time delays are selected respectively for simulation, which is shown in Figures 3-8.
It can be found from Figures 3 and 4 that in the case of selecting different initial values, the curves of solutions for the drive-response systems (4.1) and (4.3) tend to be consistent, and the error curves of the solutions of the systems (4.1) and (4.3) tend to zero. From Figures 5 and 6, it is easy to see that in the case of selecting different fractional orders, the curves of solutions for the drive-response systems (4.1) and (4.3) tend to be consistent, and the error curves of the solutions of systems (4.1) and (4.3) tend to zero. It can also be seen from Figures 7 and 8, in the case of selecting different time delays, the curves of solutions for the drive-response systems (4.1) and (4.3) tend to be consistent, and the error curves of the solutions of the systems (4.1) and (4.3) tend to zero.
In summary, when different initial conditions, different fractional orders, and different time delays are selected respectively for simulation, the error curves eventually tend to zero, which verifies that the drive system (4.1) is globally asymptotically synchronized with the response system (4.3), and the initial conditions, the fractional orders and time delays only change the synchronization time, but not the synchronization behavior of the drive-response systems (4.1) and (4.3).
Next, some comparison experiments are given to show the performances of the proposed methods in this paper. Figures 9-14 are the experiment results based on the controller in reference [8]. By comparing Figures 3-8 and Figures 9-14, we can clearly see that the synchronization time of the controller in this paper is less than that of the controller in reference [8]. In addition, Figures 15 and 16 show the experimental results of the fractional derivatives with an order greater than 1 based on the controller in this paper. From the experimental results in Figures 15 and 16, it can be seen that when the derivative order is greater than 1, the drive-response system is not synchronized.
4.
Conclusion
In this article, a class of delayed nonautonomous FO neural networks with Caputo derivatives is considered and the global synchronization problem of the above system is studied. Firstly, new FO neural networks are proposed by introducing variable parameters into known models, and the analytical formula of the synchronous controller is given according to the new neural networks. Secondly, from the drive-response systems corresponding to the above delayed FO neural networks, their error system is obtained. Thirdly, by constructing the Lyapunov function and utilizing the Razumikhin-type stability theorem, the asymptotic stability of zero solution for the error system is verified, and some sufficient conditions are achieved to ensure the global synchronization of studied neural networks. Finally, some numerical simulations are presented to show the availability and feasibility of our theoretical results. The theoretical results obtained in this article not only can effectively determine the synchronization of the new FO neural networks but also improve and extend some existing results [8,12,13,21].
Acknowledgments
This work is supported by General Projects of Local Science and Technology Development Funds Guided by the Central Government (Grant No: 2022ZYD0005), Key Project of Scientific Research and Innovation Team of Chengdu University of Information Technology(Grant No: KYTD202226), and the Scientific Research Fund of Chengdu University of Information Technology of China (Grant no. KYTZ201820).
Conflicts of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad:

















