1.
Introduction
With the development of artificial intelligence, multi-agent systems have attracted extensive attention of researchers in computer science, physics, biology, social science and control engineering. The design of multi-agent systems is greatly influenced by the collective behaviour of animals in nature, such as ant colony gathering, birds flocking and fish swarming. Generally, a multi-agent system consists of multiple independent autonomous or semi-autonomous agents interconnected through a communication network, with research focuses including consensus [1], flocking [2], swarming [3], collision avoiding [4,5], formation control [6,7] and event-triggered control [8,9] etc. Consensus describes the process of agents coordination which has important applications in opinion dynamics and engineering control, and has been thoroughly analysed yielding a number of conditions guaranteeing that the agents reach consensus in the past decade, see [10,11,12,13,14].
The early literature on consensus has mainly focused on the analysis of autonomous systems whose final state after reaching consensus depends only on the initial configuration of the system. However, the application of autonomous system is limited because it is inconvenient and inflexible to use the target state to design the initial configuration of the system when the system is required to reach a specified state. One type of intervention, adding external forces to the system to reach the desired target state, is applicable to a variety of real-world contexts, such as financial markets, public opinion and a team of UAVs, and has been prevalent in multi-agent systems. Further, such interventions usually only affect a subset of individuals in the system, resulting in the leader-follower structure of multi-agent systems [15,16,17].
In a multi-agent system with leader-follower structure, the leaders refer to the part of agents who master information about the target state (i.e., those affected by the intervention), and the rest of the agents in the system is called followers. Leaders should not only carry out the information communication among the agents in the system, but also track the target state, while followers only are required to join in the information communication. In most previous researches, the information communication and the target tracking were separated, and the strength of target tracking was assumed to be finite based on the actual situation that the external force is limited by energy, equipment and technology.
Different from the above studies, this paper focuses more on the agent performance than on the external force. Considering the limited ability of agents, we assume that each agent has a task strategy to properly allocate its limited energy for the information communication and the target tracking. The detail of the first-order multi-agent system involving task strategies αi∈[0,m](i=1,2,⋯,N), is as follows:
where xi(t) is the position of the ith agent, x0(t) is the target state satisfying ˙x0(t)=f(t), t≥0, f(t)∈C([0,∞),R), m∈R+ represents the maximal strength of the information communication. For the ith agent, the strength of the information communication is m−αi and the strength of the target tracking is αi. If αi>0, the ith agent is a leader, otherwise a follower. α=∑iαi is called the total strength of the target tracking of the system. The concept of the above strategy was proposed by Piccoli et al. [18] in 2016. They considered strategies {αi}Ni=1 as controls and focused on finding optimal control strategies {αi}Ni=1 to minimize the cost 1N∑Ni=1‖xi(T)−x0(T)‖, where T>0 was the final time. The Eq (1.1) with the non-linear information communication was investigated in [19], and the sufficient conditions were proposed to guarantee that the system achieves consensus. In addition to the first-order system (1.1), this paper also focuses on the second-order multi-agent system involving task strategies, written as
where γ∈[0,1] is the weight coefficient of velocities information, which measures the proportion of the velocities information in the control. Then the weight coefficient of positions information is 1−γ. x0(t) is the target state satisfying ˙x0(t)=v0(t), ˙v0(t)=g(t), t≥0, g(t)∈C([0,∞),R). Then, we present the mathematical definition of the consensus of the system for Eqs (1.1) and (1.2).
Definition 1.1. Suppose {xi(t)}Ni=1 is a solution of the Eq (1.1), x0(t) is the target state satisfying ˙x0(t)=f(t), t≥0, f(t)∈C([0,∞),R). The Eq (1.1) is said to achieve consensus and reach the target state if and only if
Suppose {xi(t)}Ni=1 is a solution of the Eq (1.2), x0(t) is the target state satisfying ˙x0(t)=v0(t), ˙v0(t)=g(t), t≥0, g(t)∈C([0,∞),R). The Eq (1.2) is said to achieve consensus and reach the target state if and only if
The time delay is an important topic in the research of multi-agent systems and has been widely studied. The causes of the time delay can be divided into two types: information transmission delay and information processing delay. The transmission delay means that it takes time for agents to receive information from others limited by the speed of communication, see [20,21,22]. The processing delay, also known as the reaction delay, refers to the time required for devices to process information, see [23,24,25]. The effect of time delay on consensus formation of multi-agent systems is an issue that cannot be ignored. Olfsti-Saber and Murray [26] gave a sufficient condition of consensus for a first-order system with time delay on balanced graphs and showed that there exists a trade-off between the control gain and the critical delay. Yu et al. [27] obtained some necessary and sufficient conditions for second-order consensus on directed graphs. Ma et al. studied a second-order consensus system with unstable elements over undirected graphs and maximized the critical delay by optimizing parameters [28]. A first-order consensus system with unstable elements over directed graphs was investigated in [29] and maximal critical delay was achieved through solving a nonsmooth max-min problem. For other relevant literature, see [30,31,32].
In this paper, we study the effect of the processing delay on the consensus of the first-order system in Eq (1.1) and the second-order system in Eq (1.2), and analyse the relationship between the processing delay and the strategies. According to the stability of linear systems in the theory of functional differential equations, the system would achieve consensus by ensuring that roots of the characteristic equation of the system have negative real parts. The specific content of the conclusion of stability is written as:
Lemma 1.2. [33] For a linear functional equation ˙u(t)=Au(t−r)+Bu(t−s), where u(t)∈RN, A,B∈RN×N and r,s∈R+. Its characteristic equation is h(λ)=Det(λI−Ae−λr−Be−λs)=0. Define a=sup{Reλ:h(λ)=0}, if a<0, the zero solution of the equation is globally asymptotically stable.
The rest of this paper is organized as follows. In Section 2, the Eq (1.1) with a single delay is investigated. Using the continuous dependence of the equation on the processing delay, we obtain the critical delay τ∗ that ensures that the Eq (1.1) achieves consensus, show that the critical delay τ∗ of the Eq (1.1) is independent of the strategies αi. In Section 3, the Eq (1.2) with two different delays is investigated. Inspired by [34,35,36] and using the properties of plane geometry, we identify the critical region D in R2 that guarantees the system to achieve consensus, find that the shape of the critical region D is affected by the strategies αi. In Section 4, several numerical simulations are presented to explain our results. Finally, we give the conclusion and discussion in Section 5.
2.
The critical delay of the first-order multi-agent system
Adding the processing delay in the Eq (1.1) yields
where τ∈R+ represents the time required for the system to process the information of positions. Next we will transform the consensus problem of the Eq (2.1) into the stability problem of a linear autonomous system with a single delay, which further becomes the problem of judging whether the roots of the characteristic equation have negative real parts. Set yi(t)=xi(t)−x0(t), then the above model reduces to
Define
then rewrite the above equations in matrix form
Compute the eigenvalues of the matrix Γ
where α=∑Ni=1αi. Note that rank(Γ)=1, hence the matrix Γ is similarly diagonalized, i.e., there exists a non-singular matrix P such that PΓP−1=J, where J=diag(m−αN,0,⋯,0). Let Z(t)=PY(t), then the equation becomes
The characteristic equation of the above system is
Hence, applying Lemma 1.2 we know that the Eq (2.1) achieves consensus if all roots of the Eq (2.3) have negative real parts. Using the continuous dependence of the Eq (2.3) on the processing delay τ, we obtain the following result.
Theorem 2.1. Assume α>0. Let Λ=sup{Reλ:h(λ)=0}, then there exists a critical delay
such that Λ<0, ∀0≤τ<τ∗.
Proof. Owing to m,αN,τ∈R, ¯h(−iω)=h(iω), ∀ω∈R, which means that if λ=iω is a root of Eq (2.3), then also λ=−iω is a root. Without loss of generality let h(iω)=0, ω∈R+, then we obtain
From iω+me−iωτ=0 we have mcos(ωτ)=0 and ω=msin(ωτ). Adding the squares of the two equations yields ω=m, then we have τkm=π2m+kπm, k∈Z. Similarly, from iω+αNe−iωτ=0 we could obtain τkα=πN2α+kπNα, k∈Z. Define
When τ=0,
By α>0, Λ<0 which indicates that all roots of the Eq (2.3) lie on the left half complex plane when τ=0. Since h(λ) is continuously dependent on τ, Λ is continuously dependent on τ. Therefore, as the increase of τ from 0 to ∞, some roots of the Eq (2.3) touch the imaginary axis of the complex plane for the first time when τ=τ∗. Then, we conclude that Λ<0 if 0≤τ<τ∗ and Λ=0 if τ=τ∗.
Remark 1. Theorem 2.1 shows that the critical delay of the Eq (2.1) has nothing to do with strategies αi, but only with the maximal strength m.
Remark 2. If Λ<0 when τ=0, then the existence of the critical delay τ∗ is equivalent to the existence of some roots of the Eq (2.3) crossing the imaginary axis of the complex plane as the increase of τ from 0 to ∞. If the critical delay τ∗ exists, then it is the value of the delay when these roots first touch the imaginary axis.
3.
The critical region of the second-order multi-agent system
Different from the Eq (1.1), the Eq (1.2) has to process not only the information of positions but also the information of velocities, so there are two different processing delays in the system. Adding the processing delay in the Eq (1.2) yields
where τ1 and τ2 represent times required for the system to process the information of positions and velocities, respectively. Similarly, we will transform the consensus problem of the Eq (3.1) into the stability problem of a linear autonomous system with two different delay. Set yi(t)=xi(t)−x0(t), the above model is simplified as
Define Y(t) and Γ same as Eq (2.2), then rewrite the equations in matrix form
Let Z(t)=PY(t), then the above equation becomes
The characteristic equation of the above system is
Let Λ=sup{Reλ:h(λ)=0}. When τ1=τ2=0, we have
If α>0, it's easy to verify that Λ<0. Next, we firstly consider three simple cases: (1) τ1>0 and τ2=0; (2) τ1=0 and τ2>0; (3) τ1=τ2>0.
Theorem 3.1. Assume α>0, 0<γ<1. If one of the following three cases holds:
(1)
(2)
(3)
Then Λ<0.
Proof. Because the proofs of (1) and (2) are very similar to the proof of (3), we will just prove the case τ1=τ2=τ>0 here. Without loss of generality let h(iω)=0, ω∈R+, then we have
or
According to the Eq (3.3) we obtain
Adding the squares of the above two equations yields
then we have
On the other hand, the second equation of Eq (3.5) gives
In the same way, according to the Eq (3.4) we could obtain
The critical delay τ∗=min{τm,τα}, so we need to determine the monotonicity of the function
Because √γ2s22+√(1−γ)2s2+γ4s44 is monotonically increasing with respect to s and arctanξξ is monotonically decreasing with respect to ξ, J(s) is monotonically decreasing with respect to s. Hence, we conclude τ∗=τm.
Remark 3. For the case (2), we cannot determine the monotonicity of the function
with respect to s. Actually, the numerical curve of J(s) shows that J(s) is monotonically increasing with respect to s. In addition, we assume 0<γ<1 in Theorem 3.1. By simple calculation we could obtain that if γ=1, the critical delay of τ1 is π2m; If γ=0, the critical delay of τ2 is π√m.
In the following we consider the case τ1≠τ2. In this case, the method applied in Theorems 2.1 and 3.1 is no longer feasible because we cannot obtain an explicit expression of τ∗ by solving for ω. Now we use a geometric method to analyse the Eq (3.2). From Eq (3.2) we have
or
Since λ=0 is not a root of the above equations, the deformations of the equations are
and
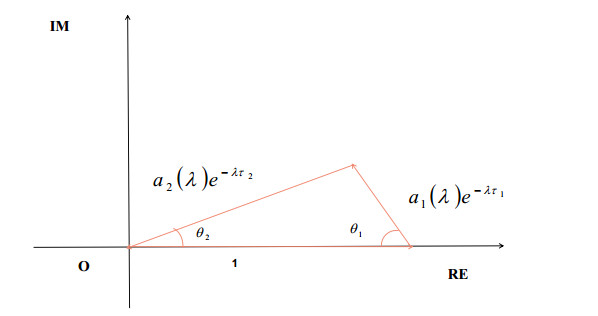
For the Eq (3.6), let a1(λ)=γmλ and a2(λ)=(1−γ)mλ2. Think of 1, a1(λ)e−λτ1 and a2(λ)e−λτ2 as three vectors in the complex plane C, then λ is a root of the Eq (3.6) if and only if the three vectors are connected head to tail to form a triangle in the complex plane (See Figure 1).
Therefore, we could use the triangle property to get the relationship between λ, τ1 and τ2, and try to obtain the critical delay.
Theorem 3.2. Assume α>0, 0<γ<1. Then there exists a connected region D⊆R+×R+ such that Λ<0, ∀(τ1,τ2)∈D. In addition, the connected region D and its boundary ∂D satisfy
where
τ∗1, τ∗2 and τ∗ are defined in Theorem 3.1, θ1, θ2, u±0, v∓0, Ω, ϑ1, ϑ2, p±0, q∓0 and Υ are defined in the proof.
Proof. The proof is divided into three steps.
The first step: use the triangle inequality to obtain the range of ω such that h(iω)=0. Without loss of generality let λ=iω, ω∈R+, then from Eq (3.6) we have
where a1(iω)=−γmωi and a2(iω)=−(1−γ)mω2. According to the triangle inequality that the length of any one side does not exceed the sum of the other two sides, we obtain
i.e.
Denoting the range of ω by Ω and solving the inequalities yields
Ω contains all the values of ω that make the roots of the Eq (3.6) lie on the imaginary axis of the complex plane at iω.
The second step: use Ω to calculate all the values of (τ1,τ2)∈R+×R+ that make h(iω)=0. Define ∡a1(iω)∈[0,2π) is the angle between a1(iω) with the positive direction of the real axis, θ1∈[0,π] is the inner angle of the triangle formed by a1(iω)e−iωτ1 and 1. Similar definitions apply to ∡a2(iω)∈[0,2π) and θ2∈[0,π]. Because a1(iω)=−γmωi and a2(iω)=−(1−γ)mω2, ∡a1(iω)=3π2 and ∡a2(iω)=π. By the law of cosine we have
Using properties of plane geometry we know that the angle between a1(iω)e−iωτ1 with the positive direction of the real axis plus or minus θ1 is equal to π, where plus or minus depends on whether the triangle is above or below the real axis. Similar results apply to a2(iω)e−iωτ2 and θ2. Then, we could establish the relations between τ1 with ω and τ2 with ω respectively:
where −ωτ1+2uπ∈[0,2π) is the angle between e−iωτ1 with the positive direction of the real axis, −ωτ2+2vπ∈[0,2π) is the angle between e−iωτ2 with the positive direction of the real axis. Define u±0 and v∓0 are the smallest positive integers to guarantee τ1>0 and τ2>0 respectively, then we obtain
Define
then Φ⊆R+×R+ contains all the values of (τ1,τ2)⊆R+×R+ that make the roots of the Eq (3.6) lie on the imaginary axis.
Repeating the above steps for the Eq (3.7) yields that the roots of the Eq (3.7) lie on the imaginary axis if and only if (τ1,τ2)∈Ψ, where
Hence, we proved that some roots of the Eq (3.2) lie on the imaginary axis if and only if (τ1,τ2)∈Φ∪Ψ.
The third step: combine Theorem 3.1 and Φ∪Ψ to determine the connected region D. By the results in [35,37], Φ∪Ψ characterizes a series of continuous curves on R+×R+ and divides R+×R+ into a series of connected regions. Let D represent the connected region containing the origin (0,0), then Theorem 3.1 indicates that the connected region D and its boundary ∂D satisfy
Because Λ<0 when (τ1,τ2)=(0,0)∈D, Λ=0 when (τ1,τ2)∈Φ∪Ψ and Λ is continuously dependent on (τ1,τ2), we conclude that Λ<0, ∀(τ1,τ2)∈D.
The the connected region D in Theorem 3.2 satisfies D1∪D2∪{(τ∗,τ∗)}⊆∂D and ∂D∖(D1∪D2)⊆Φ∪Ψ. Define the closure of D as ¯D, then we have Λ<0, ∀(τ1,τ2)∈D and Λ=0, ∀(τ1,τ2)∈¯D∖D. Hence, we call the connected region D the critical region. However, Φ∪Ψ contains so many curves that we cannot imagine the approximate range of D. By further analysing Φ∪Ψ, we will show that the critical region D is contained in a bounded region.
Theorem 3.3. Assume D is the critical region in Theorem 3.2. There exists a bounded region D∗⊆R+×R+ satisfying ∂D∗⊆D1∪D2∪C1∪C2 and ¯D∗∖D∗⊆C1∪C2 such that D⊆D∗, where
D1, D2, θ1, θ2, Ω, ϑ1, ϑ2, and Υ are defined in Theorem 3.2.
Proof. Set
If (τ1,τ2)=(0,0), then ∡b1=3π2, ∡b2=π and the positions of 1, b1 and b2 on the complex plane are shown in Figure 2 Case 1. In this case, the Eq (3.6) do not have imaginary roots so that 1, b1 and b2 do not form a triangle in the complex plane. From Theorem 3.2 we know that 1, b1 and b2 could form a triangle for any (τ1,τ2)∈Φ∪Ψ. Select curves C1 and C2 from Φ∪Ψ, where
For the curve C1, let τ1=0 yields θ1=π2, then applying the properties of right triangle we obtain 1+|a1(iω)|2=|a2(iω)|2 and tan(θ2)=|a1(iω)|, (See Figure 2 Case 2) i.e.,
Solve the above equations yields
Let τ2=0 yields θ2=0, which means that the triangle degenerates into a line segment (See Figure 2 Case 4), so we have 1=|a1(iω)|+|a2(iω)| and θ1=0, and then
Let τ1=τ2 yields θ1+θ2=π2, then we have 1=|a1(iω)|2+|a2(iω)|2 and tan(θ2)=|a1(iω)||a2(iω)| (See Figure 2 Case 3). By solving the above equation we obtain
Define a bounded region E1 formed by the curve C1 with the positive half of the horizontal and vertical axes, then the above statement indicates that D⊆E1. Similarly, For the curve C2, define a bounded region E2 formed by the curve C2 with the positive half of the horizontal and vertical axes, then we could verify that D⊆E2.
Let D∗=(E1∩E2)∖(C1∪C2), then D⊆D∗ and D is a bounded region. In addition, D∗ satisfies ∂D∗⊆D1∪D2∪C1∪C2 and ¯D∗∖D∗⊆C1∪C2.
Remark 4. Theorem 3.3 indicates that (τ∗1,0),(τ∗,τ∗)∈C1 and (0,τ∗2)∈C1∪C2. If curves in Φ∖C1 do not intersect the curve C1 and curves in Ψ∖C2 do not intersect the curve C2 (except at its endpoints), then D=D∗. In addition, unlike the Eq (2.1), Theorem 3.3 shows that the critical region D of the Eq (3.1) is related to both the total strength α and the maximal strength m.
4.
Numerical Simulation
In this section, a series of simulation examples are presented to illustrate Theorems 2.1, 3.1 and 3.3.
4.1. The first-order multi-agent system
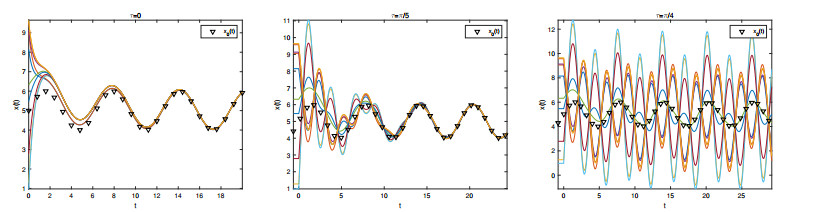
Set the target x0(t)=sin(t)+5 and f(t)=cos(t). Let N=10 and m=2, the initial positions xi(0) and strategies αi of the Eq (2.1) are listed in Table 1.
According to Theorem 2.1, the critical delay τ∗=π2m=π4. Take τ=0, τ=π5 and τ=π4 respectively to obtain simulations of the Eq (2.1) as shown in Figure 3.
4.2. The second-order multi-agent system
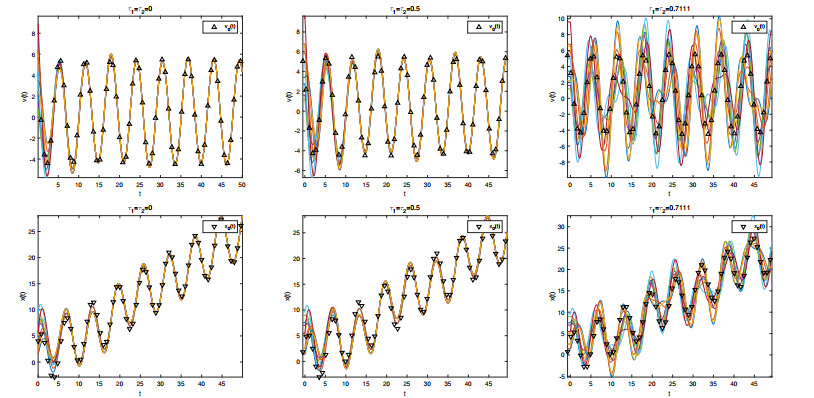
Set the target x0(t)=3sin(t)+4cos(t)+t2, v0(t)=3cos(t)−4sin(t)+12 and g(t)=−3sin(t)−4cos(t). Let N=10, m=2 and γ=0.5, the initial positions xi(0), velocities vi(t) and strategies αi of the Eq (3.1) are listed in Table 2.
According to Theorem 3.1 we have τ∗1=π1+√5, τ∗2=min{1.1506,1.0166}=1.0166, τ∗=0.7111. Take τ1=τ2=0, τ1=τ2=0.5 and τ1=τ2=0.7111 respectively to obtain simulations of the Eq (3.1) as shown in Figure 4.
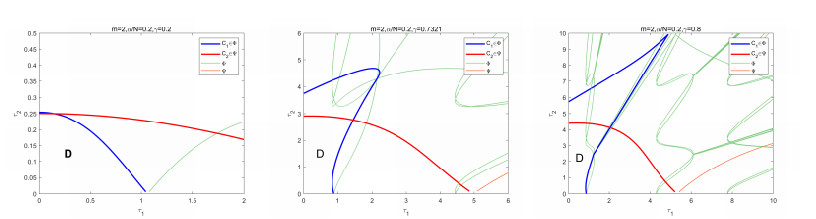
Fix m=2 and α/N=0.2, take γ=0.2, γ=0.7321 (i.e., 4(1−γ)γ2=m) and γ=0.8 respectively to obtain simulations of the Φ∪Ψ by Theorem 3.2, see Figure 5.
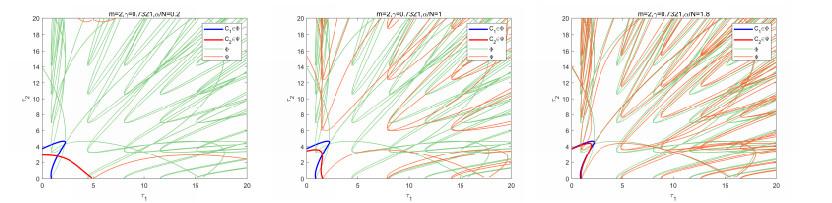
Fix m=2 and γ=0.7321, take α/N=0.2, α/N=1 and α/N=1.8 respectively to obtain simulations of the Φ∪Ψ by Theorem 3.2, see Figure 6.
5.
Conclusion and Future Direction
In this paper, we analysed the influence of the processing delay on the consensus for the first-order system in Eq (1.1) and the second-order system in Eq (1.2). For the first-order system in Eq (2.1), by the continuous dependence of the equation on τ, we obtained the critical delay τ∗ that ensures the Eq (2.1) to achieve consensus and showed that the critical delay τ∗ is independent of the strategies αi. For the second-order system in Eq (3.1), from the properties of plane geometry, we identified the critical region D in R2 that guarantees the Eq (3.1) to achieve consensus and found that the shape of the critical region D is affected by the strategies αi.
The concept of strategies αi was firstly proposed by Piccoli et al. [18] to study the problem of optimal strategy. Using Pontryagin's minimum principle in optimal control theory, they found optimal strategies {αi}Ni=1 to minimize the cost 1N∑Ni=1‖xi(T)−x0(T)‖, where T>0 was the final time. More importantly, they showed that optimal strategies are sparse. From the present work, we want to find optimal strategies αi for the Eq (2.1) and analyse the influence of delays on the selection of optimal strategies αi.
Acknowledgments
We would like to thank the editors and the reviewers for their careful reading of the paper and their constructive comments.
This work was partially supported by the National Natural Science Foundation of China (11671011) and Hunan Provincial Innovation Foundation for Postgraduate (CN) (CX20220085).
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: